我不得不說(shuō)說(shuō)卡爾曼濾波，因為它能做到的事情簡(jiǎn)直讓人驚嘆!意外的是很少有軟件工程師和科學(xué)家對對它有所了解，這讓我感到沮喪，因為卡爾曼濾波是一個(gè)如此強大的工具，能夠在不確定性中融合信息，與此同時(shí)，它提取精確信息的能力看起來(lái)不可思議。

 

什么是卡爾曼濾波?

 

你可以在任何含有不確定信息的動(dòng)態(tài)系統中使用卡爾曼濾波，對系統下一步的走向做出有根據的預測，即使伴隨著(zhù)各種干擾，卡爾曼濾波總是能指出真實(shí)發(fā)生的情況。

 

在連續變化的系統中使用卡爾曼濾波是非常理想的，它具有占用內存小的優(yōu)點(diǎn)(除了前一個(gè)狀態(tài)量外，不需要保留其它歷史數據)，并且速度很快，很適合應用于實(shí)時(shí)問(wèn)題和嵌入式系統。

 

在Google上找到的大多數關(guān)于實(shí)現卡爾曼濾波的數學(xué)公式看起來(lái)有點(diǎn)晦澀難懂，這個(gè)狀況有點(diǎn)糟糕。實(shí)際上，如果以正確的方式看待它，卡爾曼濾波是非常簡(jiǎn)單和容易理解的，下面我將用漂亮的圖片和色彩清晰的闡述它，你只需要懂一些基本的概率和矩陣的知識就可以了。

 

我們能用卡爾曼濾波做什么?

 

用玩具舉例：你開(kāi)發(fā)了一個(gè)可以在樹(shù)林里到處跑的小機器人，這個(gè)機器人需要知道它所在的確切位置才能導航。

 

 

我們可以說(shuō)機器人有一個(gè)狀態(tài)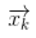，表示位置和速度：

 

 

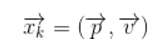
注意這個(gè)狀態(tài)只是關(guān)于這個(gè)系統基本屬性的一堆數字，它可以是任何其它的東西。在這個(gè)例子中是位置和速度，它也可以是一個(gè)容器中液體的總量，汽車(chē)發(fā)動(dòng)機的溫度，用戶(hù)手指在觸摸板上的位置坐標，或者任何你需要跟蹤的信號。

 

這個(gè)機器人帶有GPS，精度大約為10米，還算不錯，但是，它需要將自己的位置精確到10米以?xún)?。?shù)林里有很多溝壑和懸崖，如果機器人走錯了一步，就有可能掉下懸崖，所以只有GPS是不夠的。

 

 

或許我們知道一些機器人如何運動(dòng)的信息：例如，機器人知道發(fā)送給電機的指令，知道自己是否在朝一個(gè)方向移動(dòng)并且沒(méi)有人干預，在下一個(gè)狀態(tài)，機器人很可能朝著(zhù)相同的方向移動(dòng)。當然，機器人對自己的運動(dòng)是一無(wú)所知的：它可能受到風(fēng)吹的影響，輪子方向偏了一點(diǎn)，或者遇到不平的地面而翻倒。所以，輪子轉過(guò)的長(cháng)度并不能精確表示機器人實(shí)際行走的距離，預測也不是很完美。

 

GPS 傳感器告訴了我們一些狀態(tài)信息，我們的預測告訴了我們機器人會(huì )怎樣運動(dòng)，但都只是間接的，并且伴隨著(zhù)一些不確定和不準確性。但是，如果使用所有對我們可用的信息，我們能得到一個(gè)比任何依據自身估計更好的結果嗎?回答當然是YES，這就是卡爾曼濾波的用處。

 

卡爾曼濾波是如何看到你的問(wèn)題的

 

下面我們繼續以只有位置和速度這兩個(gè)狀態(tài)的簡(jiǎn)單例子做解釋。

 

 

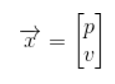
我們并不知道實(shí)際的位置和速度，它們之間有很多種可能正確的組合，但其中一些的可能性要大于其它部分：

 

 

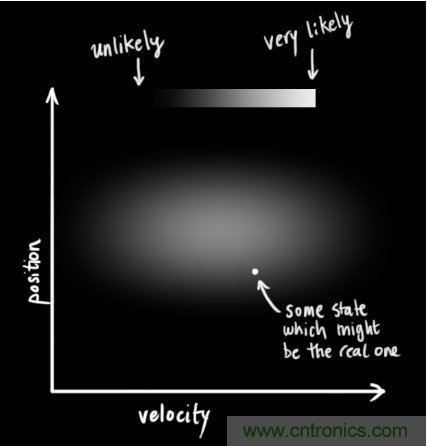
卡爾曼濾波假設兩個(gè)變量(位置和速度，在這個(gè)例子中)都是隨機的，并且服從高斯分布。每個(gè)變量都有一個(gè)均值 μ，表示隨機分布的中心(最可能的狀態(tài))，以及方差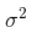，表示不確定性。

 

 

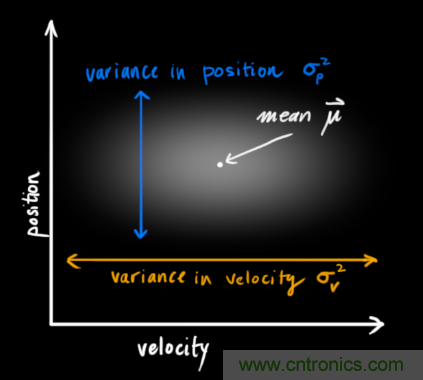
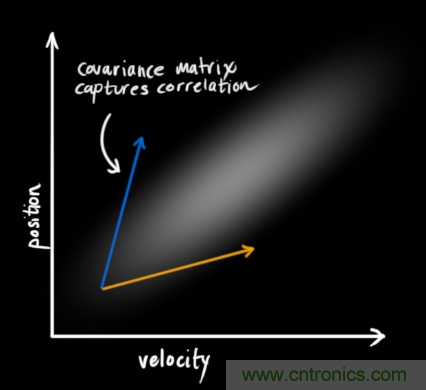
在上圖中，位置和速度是不相關(guān)的，這意味著(zhù)由其中一個(gè)變量的狀態(tài)無(wú)法推測出另一個(gè)變量可能的值。下面的例子更有趣：位置和速度是相關(guān)的，觀(guān)測特定位置的可能性取決于當前的速度：

 

 

這種情況是有可能發(fā)生的，例如，我們基于舊的位置來(lái)估計新位置。如果速度過(guò)高，我們可能已經(jīng)移動(dòng)很遠了。如果緩慢移動(dòng)，則距離不會(huì )很遠。跟蹤這種關(guān)系是非常重要的，因為它帶給我們更多的信息：其中一個(gè)測量值告訴了我們其它變量可能的值，這就是卡爾曼濾波的目的，盡可能地在包含不確定性的測量數據中提取更多信息!

 

這種相關(guān)性用協(xié)方差矩陣來(lái)表示，簡(jiǎn)而言之，矩陣中的每個(gè)元素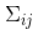表示第 i 個(gè)和第 j 個(gè)狀態(tài)變量之間的相關(guān)度。(你可能已經(jīng)猜到協(xié)方差矩陣是一個(gè)對稱(chēng)矩陣，這意味著(zhù)可以任意交換 i 和 j)。協(xié)方差矩陣通常用“”來(lái)表示，其中的元素則表示為“”。

 

 

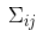使用矩陣來(lái)描述問(wèn)題

 

我們基于高斯分布來(lái)建立狀態(tài)變量，所以在時(shí)刻 k 需要兩個(gè)信息：最佳估計(即均值，其它地方常用 μ 表示)，以及協(xié)方差矩陣。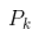

 

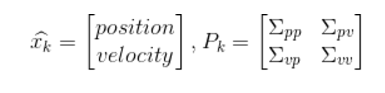     (1)

 

(當然，在這里我們只用到了位置和速度，實(shí)際上這個(gè)狀態(tài)可以包含多個(gè)變量，代表任何你想表示的信息)。接下來(lái)，我們需要根據當前狀態(tài)(k-1 時(shí)刻)來(lái)預測下一狀態(tài)(k 時(shí)刻)。記住，我們并不知道對下一狀態(tài)的所有預測中哪個(gè)是“真實(shí)”的，但我們的預測函數并不在乎。它對所有的可能性進(jìn)行預測，并給出新的高斯分布。

 

 

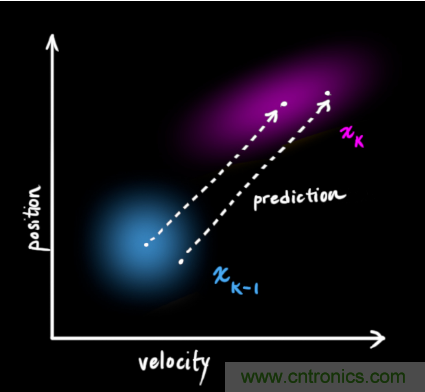
我們可以用矩陣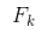來(lái)表示這個(gè)預測過(guò)程：

 

 

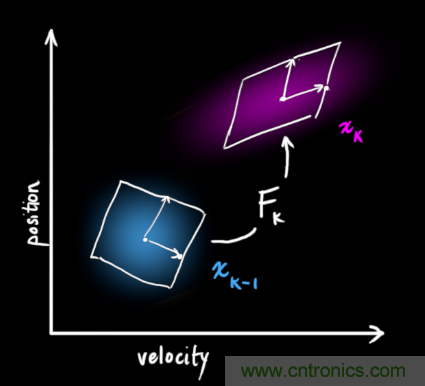
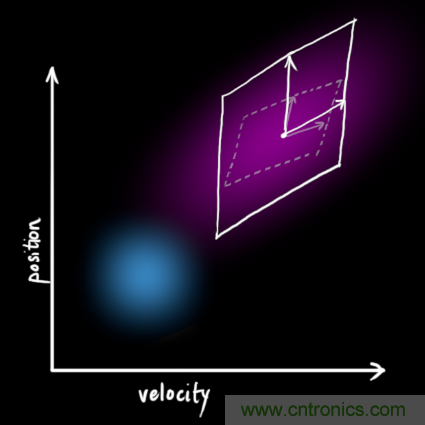
它將我們原始估計中的每個(gè)點(diǎn)都移動(dòng)到了一個(gè)新的預測位置，如果原始估計是正確的話(huà)，這個(gè)新的預測位置就是系統下一步會(huì )移動(dòng)到的位置。那我們又如何用矩陣來(lái)預測下一個(gè)時(shí)刻的位置和速度呢?下面用一個(gè)基本的運動(dòng)學(xué)公式來(lái)表示：

 

 

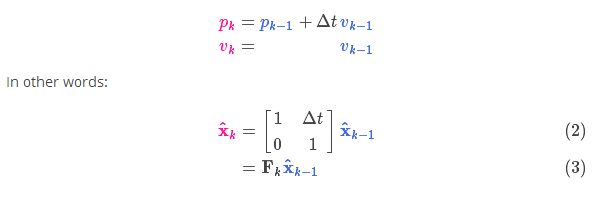
現在，我們有了一個(gè)預測矩陣來(lái)表示下一時(shí)刻的狀態(tài)，但是，我們仍然不知道怎么更新協(xié)方差矩陣。此時(shí)，我們需要引入另一個(gè)公式，如果我們將分布中的每個(gè)點(diǎn)都乘以矩陣 A，那么它的協(xié)方差矩陣會(huì )怎樣變化呢?很簡(jiǎn)單，下面給出公式：

 

 

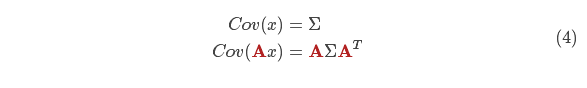
結合方程(4)和(3)得到：

 

 

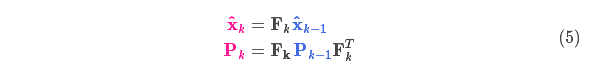
外部控制量

 

我們并沒(méi)有捕捉到一切信息，可能存在外部因素會(huì )對系統進(jìn)行控制，帶來(lái)一些與系統自身狀態(tài)沒(méi)有相關(guān)性的改變。

 

以火車(chē)的運動(dòng)狀態(tài)模型為例，火車(chē)司機可能會(huì )操縱油門(mén)，讓火車(chē)加速。相同地，在我們機器人這個(gè)例子中，導航軟件可能會(huì )發(fā)出一個(gè)指令讓輪子轉向或者停止。如果知道這些額外的信息，我們可以用一個(gè)向量來(lái)表示，將它加到我們的預測方程中做修正。

 

假設由于油門(mén)的設置或控制命令，我們知道了期望的加速度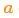，根據基本的運動(dòng)學(xué)方程可以得到：

 

 

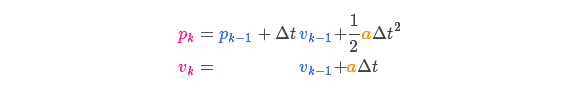
以矩陣的形式表示就是：

 

 

稱(chēng)為控制矩陣，稱(chēng)為控制向量(對于沒(méi)有外部控制的簡(jiǎn)單系統來(lái)說(shuō)，這部分可以忽略)。讓我們再思考一下，如果我們的預測并不是100%準確的，該怎么辦呢?

 

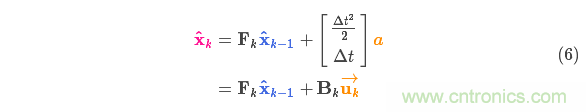
外部干擾

 

如果這些狀態(tài)量是基于系統自身的屬性或者已知的外部控制作用來(lái)變化的，則不會(huì )出現什么問(wèn)題。

 

但是，如果存在未知的干擾呢?例如，假設我們跟蹤一個(gè)四旋翼飛行器，它可能會(huì )受到風(fēng)的干擾，如果我們跟蹤一個(gè)輪式機器人，輪子可能會(huì )打滑，或者路面上的小坡會(huì )讓它減速。這樣的話(huà)我們就不能繼續對這些狀態(tài)進(jìn)行跟蹤，如果沒(méi)有把這些外部干擾考慮在內，我們的預測就會(huì )出現偏差。

 

在每次預測之后，我們可以添加一些新的不確定性來(lái)建立這種與“外界”(即我們沒(méi)有跟蹤的干擾)之間的不確定性模型：

 

 

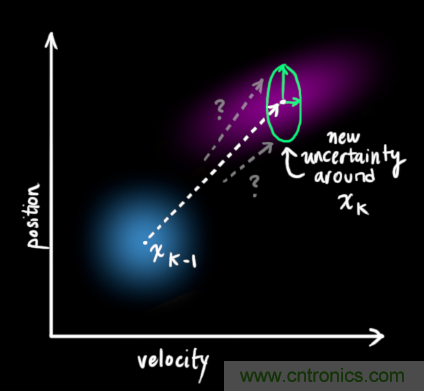
原始估計中的每個(gè)狀態(tài)變量更新到新的狀態(tài)后，仍然服從高斯分布。我們可以說(shuō)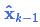的每個(gè)狀態(tài)變量移動(dòng)到了一個(gè)新的服從高斯分布的區域，協(xié)方差為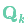。換句話(huà)說(shuō)就是，我們將這些沒(méi)有被跟蹤的干擾當作協(xié)方差為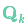的噪聲來(lái)處理。

 

 

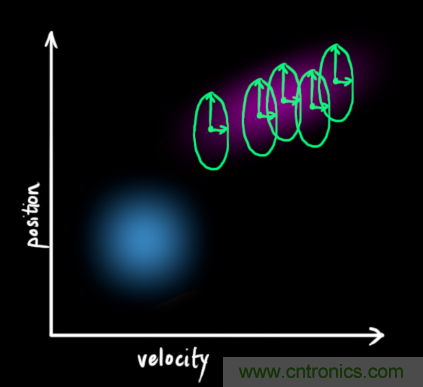
這產(chǎn)生了具有不同協(xié)方差(但是具有相同的均值)的新的高斯分布。

 

 

我們通過(guò)簡(jiǎn)單地添加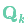得到擴展的協(xié)方差，下面給出預測步驟的完整表達式：

 

 

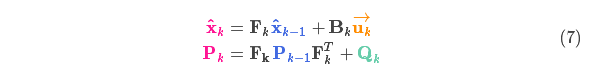
由上式可知，新的最優(yōu)估計是根據上一最優(yōu)估計預測得到的，并加上已知外部控制量的修正。

 

而新的不確定性由上一不確定性預測得到，并加上外部環(huán)境的干擾。

 

好了，我們對系統可能的動(dòng)向有了一個(gè)模糊的估計，用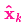和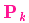來(lái)表示。如果再結合傳感器的數據會(huì )怎樣呢?

 

用測量值來(lái)修正估計值

 

我們可能會(huì )有多個(gè)傳感器來(lái)測量系統當前的狀態(tài)，哪個(gè)傳感器具體測量的是哪個(gè)狀態(tài)變量并不重要，也許一個(gè)是測量位置，一個(gè)是測量速度，每個(gè)傳感器間接地告訴了我們一些狀態(tài)信息。

 

 

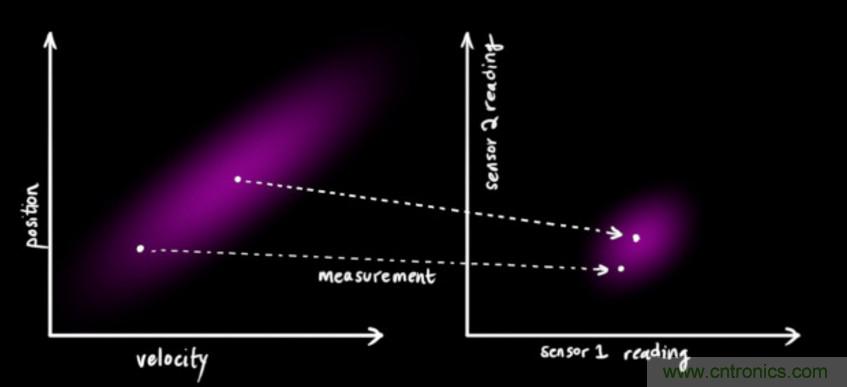
注意，傳感器讀取的數據的單位和尺度有可能與我們要跟蹤的狀態(tài)的單位和尺度不一樣，我們用矩陣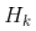來(lái)表示傳感器的數據。

 

 

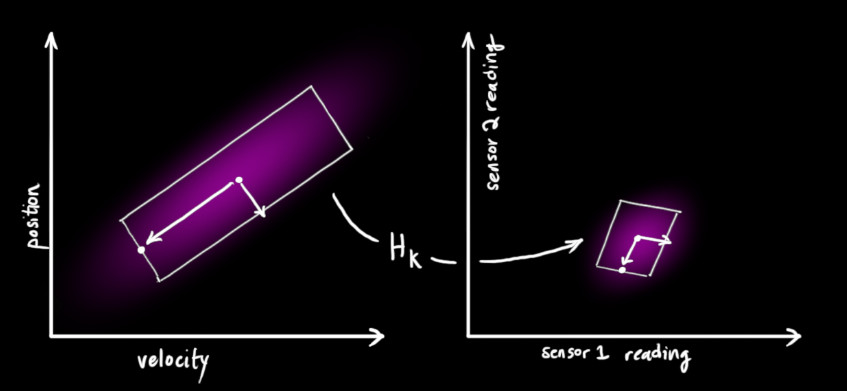
我們可以計算出傳感器讀數的分布，用之前的表示方法如下式所示：

 

 

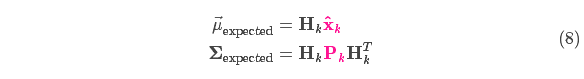
卡爾曼濾波的一大優(yōu)點(diǎn)就是能處理傳感器噪聲，換句話(huà)說(shuō)，我們的傳感器或多或少都有點(diǎn)不可靠，并且原始估計中的每個(gè)狀態(tài)可以和一定范圍內的傳感器讀數對應起來(lái)。

 

 

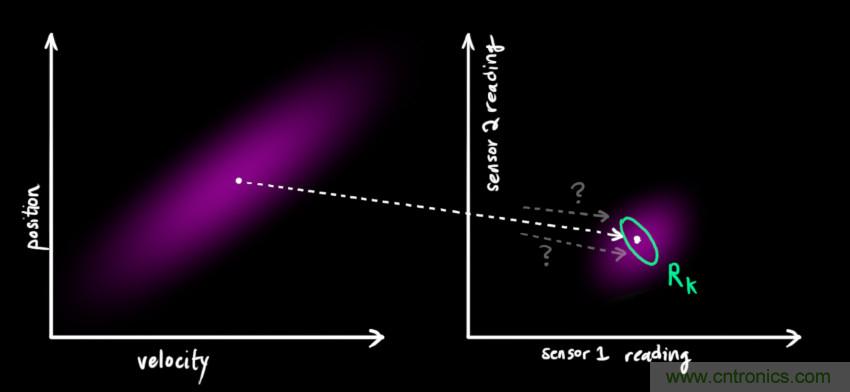
從測量到的傳感器數據中，我們大致能猜到系統當前處于什么狀態(tài)。但是由于存在不確定性，某些狀態(tài)可能比我們得到的讀數更接近真實(shí)狀態(tài)。

 

 

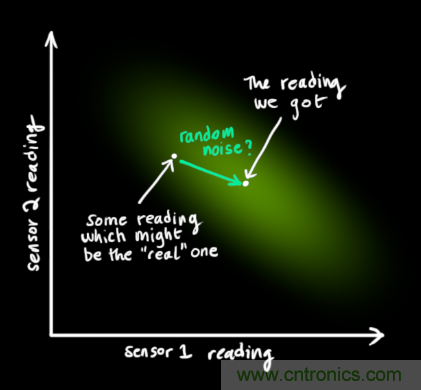
我們將這種不確定性(例如：傳感器噪聲)用協(xié)方差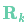表示，該分布的均值就是我們讀取到的傳感器數據，稱(chēng)之為。

 

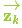現在我們有了兩個(gè)高斯分布，一個(gè)是在預測值附近，一個(gè)是在傳感器讀數附近。

 

 

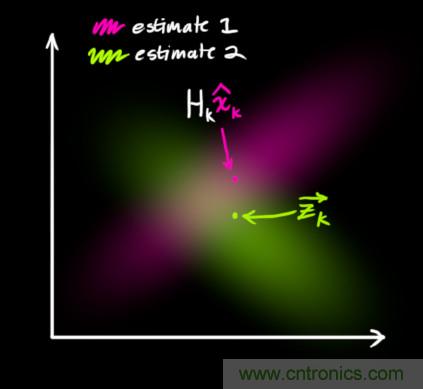
我們必須在預測值(粉紅色)和傳感器測量值(綠色)之間找到最優(yōu)解。

 

那么，我們最有可能的狀態(tài)是什么呢?對于任何可能的讀數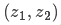，有兩種情況：(1)傳感器的測量值;(2)由前一狀態(tài)得到的預測值。如果我們想知道這兩種情況都可能發(fā)生的概率，將這兩個(gè)高斯分布相乘就可以了。

 

 

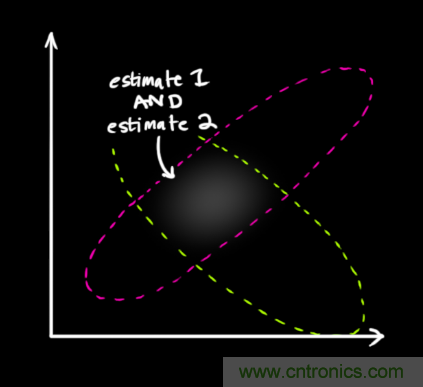
剩下的就是重疊部分了，這個(gè)重疊部分的均值就是兩個(gè)估計最可能的值，也就是給定的所有信息中的最優(yōu)估計。

 

瞧!這個(gè)重疊的區域看起來(lái)像另一個(gè)高斯分布。

 

 

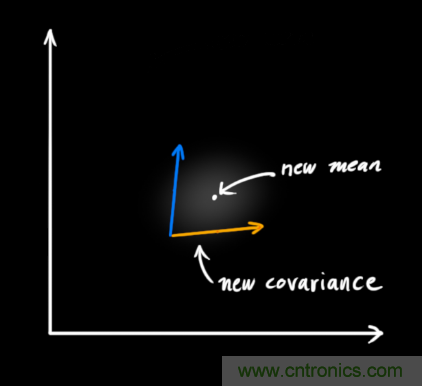
如你所見(jiàn)，把兩個(gè)具有不同均值和方差的高斯分布相乘，你會(huì )得到一個(gè)新的具有獨立均值和方差的高斯分布!下面用公式講解。

 

融合高斯分布

 

先以一維高斯分布來(lái)分析比較簡(jiǎn)單點(diǎn)，具有方差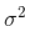和 μ 的高斯曲線(xiàn)可以用下式表示：

 

 

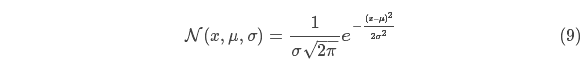
如果把兩個(gè)服從高斯分布的函數相乘會(huì )得到什么呢?

 

 

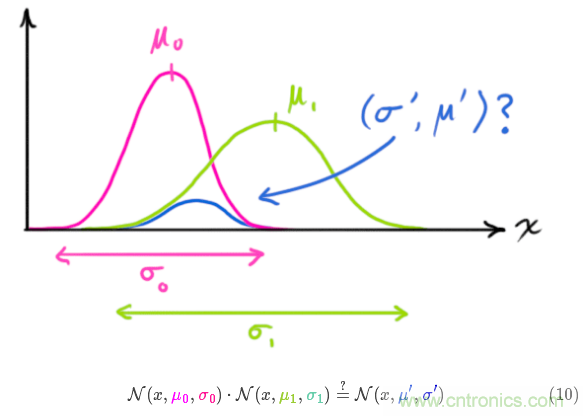
將式(9)代入到式(10)中(注意重新歸一化，使總概率為1)可以得到：

 

 

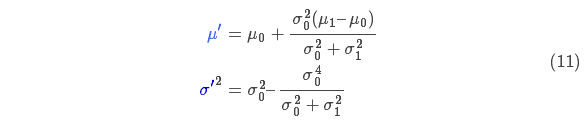
將式(11)中的兩個(gè)式子相同的部分用 k 表示：

 

 

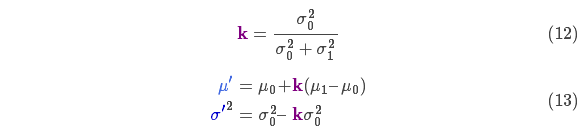
下面進(jìn)一步將式(12)和(13)寫(xiě)成矩陣的形式，如果 Σ 表示高斯分布的協(xié)方差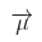，表示每個(gè)維度的均值，則：

 

 

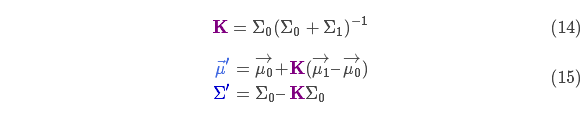
矩陣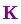稱(chēng)為卡爾曼增益，下面將會(huì )用到。放松!我們快要完成了!

 

將所有公式整合起來(lái)

 

我們有兩個(gè)高斯分布，預測部分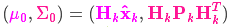，和測量部分，將它們放到式(15)中算出它們之間的重疊部分：

 

 

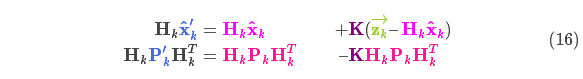
由式(14)可得卡爾曼增益為：

 

 

將式(16)和式(17)的兩邊同時(shí)左乘矩陣的逆(注意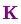里面包含了)將其約掉，再將式(16)的第二個(gè)等式兩邊同時(shí)右乘矩陣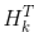的逆得到以下等式：

 

 

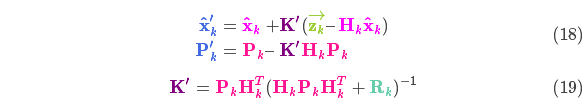
上式給出了完整的更新步驟方程。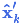就是新的最優(yōu)估計，我們可以將它和放到下一個(gè)預測和更新方程中不斷迭代。

 

 

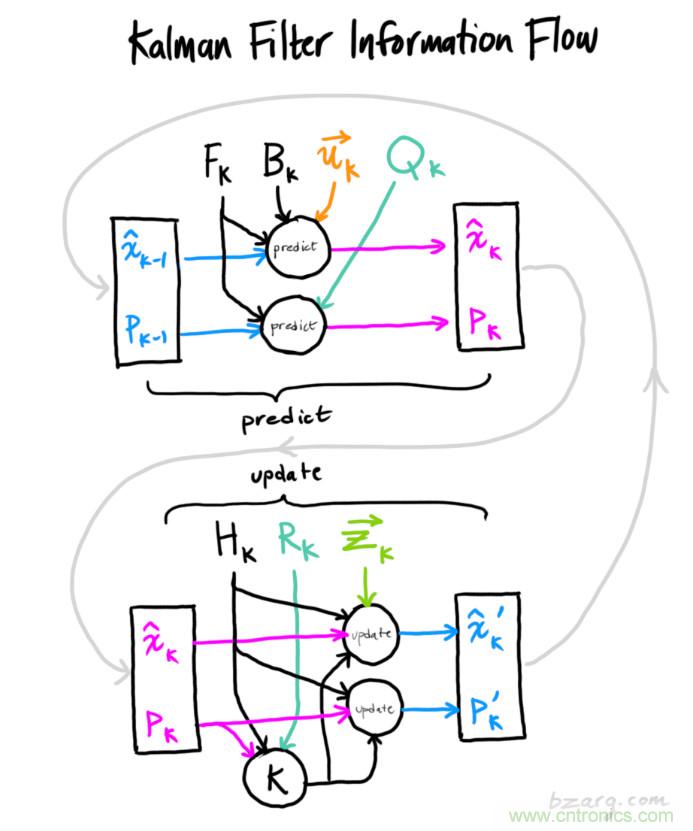
總結

 

以上所有公式中，你只需要用到式(7)、(18)、(19)。(如果忘了的話(huà)，你可以根據式(4)和(15)重新推導一下)

 

我們可以用這些公式對任何線(xiàn)性系統建立精確的模型，對于非線(xiàn)性系統來(lái)說(shuō)，我們使用擴展卡爾曼濾波，區別在于EKF多了一個(gè)把預測和測量部分進(jìn)行線(xiàn)性化的過(guò)程。

 

本文轉載自電子工程專(zhuān)輯。

 

 

推薦閱讀：