由于典型的運算放大器中包含大量有源器件，僅使用晶體管級模型的電路仿真會(huì )消耗大量時(shí)間，特別是電路中包含多個(gè)運算放大器時(shí)。由于涉及多個(gè)非線(xiàn)性方程，即使是簡(jiǎn)單的半導體器件模型也會(huì )消耗大量計算時(shí)間。在某些情況下，完成整個(gè)仿真所需的時(shí)間可能超過(guò)構建工程原型所需的時(shí)間。顯然，這種情況完全背離了使用SPICE的初衷。

 

幸運的是，我們可以通過(guò)使用盡可能準確地表示運算放大器的宏模型來(lái)縮短仿真時(shí)間，而無(wú)需使用大量晶體管或其他非線(xiàn)性器件。然而，無(wú)論出于何種意圖和目的，要設計一個(gè)能完全模擬實(shí)際器件的宏模型是一個(gè)相當大的挑戰。對于電路設計人員來(lái)說(shuō)，運算放大器模型要切實(shí)起到作用，則不能只涵蓋所有重要的DC參數，還要能夠在遠超單位增益交越頻率的區域內合理地仿真近似AC特性。

 

現有的宏模型是不夠的

 

許多運算放大器的宏模型已包含在多個(gè)可用軟件仿真器的器件庫中。這些模型大多數都是基于Graeme Boyle和他的同事（見(jiàn)參考文獻1）所做的初期工作，他們在20世紀70年代中期開(kāi)發(fā)了一些宏模型，以緩解當時(shí)已經(jīng)超負荷的大型計算機的CPU時(shí)間緊張問(wèn)題。Boyle幾乎去除了宏模型中的所有晶體管，只保留了兩個(gè)晶體管。保留的這兩個(gè)器件構成了運算放大器的差分輸入級；后續的所有級都采用線(xiàn)性控制源、無(wú)源元件和二極管來(lái)實(shí)現。輸入級中保留的晶體管有助于仿真實(shí)際影響，例如偏置電流，以及輸出dV/dt隨差分輸入電壓的變化。

 

Boyle方法大大減少了所有非線(xiàn)性元件的數量，所以每個(gè)放大器所需的仿真時(shí)間也大幅縮短。相比完全采用晶體管的仿真，Boyle結構確實(shí)有明顯改善，但該結構仍有一些不足之處，這也促進(jìn)了新的宏模型的開(kāi)發(fā)。該結構具有以下缺陷：

 

-Boyle模型只提供兩個(gè)極（沒(méi)有零）來(lái)顯示整個(gè)放大器的頻率響應——這種配置僅適用于較慢的運算放大器，完全不適合如今速度更快的器件。

-所有內部產(chǎn)生的節點(diǎn)電壓都以地為基準，即使放大器相對于地“浮空”。這種配置不能體現運算放大器的真實(shí)運行狀況——幾乎所有可用的器件都不提供接地參考。

-輸出端電流從連接到地的受控源流出，而不是像在實(shí)際放大器中那樣從電源軌流出。此特性完全排除了基于放大器的輸出電流（在電源軌之間正確分流）來(lái)仿真電路的情況。

 

理想元件可以降低復雜性

 

開(kāi)發(fā)原始的Boyle模型（圖1）的電路拓撲結構時(shí)，使用了兩種基本的宏模型建模方法（稱(chēng)為簡(jiǎn)化法和構造法），這兩種方法在開(kāi)發(fā)新宏模型時(shí)也非常有用。

 

圖1：Boyle運算放大器宏模型的一個(gè)重大缺陷是所有電壓都以地為基準

 

圖2：新運算放大器宏模型本質(zhì)上是模塊化的。在運算放大器設計中，可以通過(guò)級聯(lián)任何構建模塊來(lái)獲得任意數量的極和零點(diǎn)。

 

這種簡(jiǎn)化技術(shù)使用簡(jiǎn)單的理想元件來(lái)代替電路的實(shí)際部分，從而持續降低運算放大器主要內部級的復雜性。因此，可以通過(guò)利用此方法的功能模塊來(lái)高度仿真實(shí)際電路。在圖1中，輸入級模型就是一個(gè)很好的簡(jiǎn)化示例。該模型保留了發(fā)射極耦合對的差分輸入特性，但消除了所有有源負載；它用理想元件代替尾電流源；并承擔產(chǎn)生第二放大器極的任務(wù)。增加一個(gè)電容(CE)即可使該模型在此級中提供一個(gè)極，而減少元件總數則能加快仿真運行速度。

 

另一方面，可以使用構造法構建一個(gè)完全由理想元件組成的電路模塊，高度仿真器件實(shí)際部分的行為。遺憾的是，構造法常常會(huì )導致一些子部分與實(shí)際等效部分毫不相似。圖1的輸出級就是一個(gè)很好的示例：它提供了必要的輸出電壓限幅，具有正確的輸出電阻，還提供了短路限流值；但與實(shí)際運算放大器原理圖沒(méi)有一點(diǎn)相似之處。

 

開(kāi)發(fā)改進(jìn)的宏模型

 

開(kāi)發(fā)新的宏模型（圖2）的目的是創(chuàng )建一個(gè)能夠像實(shí)際運算放大器一樣運行的模型；但它仍然必須足夠簡(jiǎn)單，可以作為一個(gè)通用模型使用。圖3、圖4和圖5顯示該模型由處理輸入信號的幾個(gè)級聯(lián)部分組成。

 

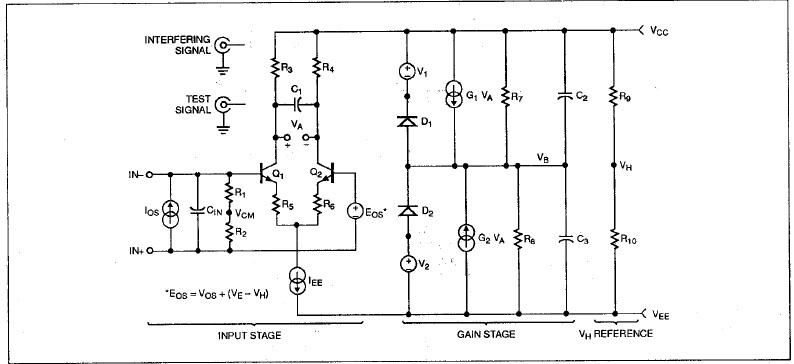
圖3：新模型的輸入級與Boyle模型的輸入級相似，但之后所有級的結構都截然不同

 

圖4：除提供零點(diǎn)的共模增益級外，還提供三種類(lèi)型的頻率成形網(wǎng)絡(luò )

 

圖5：新輸出級還配有電流源，對供電軌之間的負載電流正確分流

 

由于該模型在構建時(shí)采用了簡(jiǎn)化技術(shù)，所以其輸入級與Boyle模型非常相似。但是，由于生成新模型的剩余部分時(shí)采用了構造法，在輸入級之后，這兩個(gè)宏模型毫無(wú)任何相似之處。注意，在任何信號處理模塊中都沒(méi)有接地參考。相反，在實(shí)施差分至單端轉換后，所有內部產(chǎn)生的節點(diǎn)電壓都以供電軌之間的中點(diǎn)為基準。這個(gè)中點(diǎn)在模型中稱(chēng)為VH，由兩個(gè)連接在供電軌之間的等值電阻產(chǎn)生。

 

在使用新宏模型對任何特定的運算放大器建模時(shí)，其最低要求基本上與Boyle拓撲的要求相同：一個(gè)差分輸入級、一個(gè)增益級和一個(gè)輸出級。這種配置可以產(chǎn)生基本的雙極頻率響應，且可以從仿真時(shí)間這個(gè)角度直接比較這兩種宏模型。您可以在增益級和輸出級之間添加單位增益極、極零點(diǎn)和零極點(diǎn)模塊的任意組合，以獲得所需的頻率相關(guān)開(kāi)環(huán)增益滾降。模塊之間的區別在于：極零點(diǎn)模塊產(chǎn)生的極點(diǎn)頻率比零點(diǎn)低，而零極點(diǎn)產(chǎn)生的極點(diǎn)頻率比零點(diǎn)高。

 

框圖2“模型參數的計算”顯示了基于圖3、4和5所示的構建模塊構建運算放大器所需完成的計算。只要給出所探討的運算放大器的某些數據手冊參數，結合必要的極零點(diǎn)位置，就可以使用計算器輕松完成這些計算。

 

圖3中的輸入級是一個(gè)簡(jiǎn)化雙晶體管電路。新模型和舊模型的主要區別在于：在新模型中，輸入級使用與實(shí)際運算放大器同類(lèi)型的輸入器件，即NPN或PNP雙極性器件、P通道JFET（或者如果適用，使用N通道器件），或者M(jìn)OSFET。Boyle模型只允許在輸入級使用雙極性器件，如果是對雙極性輸入運算放大器進(jìn)行建模，這毫無(wú)問(wèn)題。但是，如果使用Boyle技術(shù)對一個(gè)FET輸入運算放大器建模，則必須大幅提高輸入晶體管的電流增益，以獲得所需的輸入偏置電流。此外還必須通過(guò)發(fā)射極負反饋來(lái)降低其跨導。這些更改導致的結果是：無(wú)法在寬輸入差分電壓范圍（一般是1至2V）內正確仿真FET輸入放大器的輸出dV/dt的常見(jiàn)變化。A降級之后的雙極輸入級具有線(xiàn)性化、雙曲正切傳遞特性（見(jiàn)文獻2），而FET輸入級具有平方律傳遞特性（見(jiàn)文獻3）。顯然，這些特性并不對等。因此，由于FET輸入級的參數計算并不比雙極性級復雜，所以在模型中使用正確的輸入器件是有意義的。

 

所有表現出非理想行為的輸入級參數（如失調電壓、失調電流和輸入電容）都使用單獨的理想元件進(jìn)行建模。此外，在反相和同相輸入端之間連接兩個(gè)等值電阻，以產(chǎn)生共模輸入電壓。模型的后續部分會(huì )用到輸入電壓，先進(jìn)行擴展和頻率成形，之后反饋到輸入級用于修正失調電壓。

 

該模型假設輸入晶體管是完全匹配的，且沒(méi)有任何會(huì )改變整體頻率響應的結電容。但是，通過(guò)為雙極性級選擇合適的電流增益，或為FET級選擇合適的柵極漏電流，它也可以得出正確的輸入偏置電流。通過(guò)使負載電阻值等于晶體管跨導的倒數，可以將差分對的電壓增益設為單位增益。這個(gè)假設簡(jiǎn)化了確定壓擺率限制元件的計算。為方便起見(jiàn)，將輸入級的尾電流標稱(chēng)值設為1 mA；但是，這個(gè)值可以降低到100µA、10µA或1µA，具體取決于放大器的總靜態(tài)電流。

 

增益級的特性

 

該模型的開(kāi)環(huán)增益通常在一個(gè)單級（見(jiàn)圖3）中實(shí)現，該級由兩個(gè)電壓控制電流源、兩個(gè)電阻、兩個(gè)電容和一個(gè)電壓限制網(wǎng)絡(luò )組成。在這個(gè)級中，也會(huì )發(fā)生差分至單端信號轉換。電壓限制網(wǎng)絡(luò )由一對二極管組成，每個(gè)二極管都連接到自己的電壓源。該網(wǎng)絡(luò )防止增益級和模型的其他內部節點(diǎn)在輸入過(guò)載驅動(dòng)條件下出現超過(guò)電源軌電壓的擺幅。在開(kāi)環(huán)增益級必須限制電壓；否則，后續節點(diǎn)可能會(huì )嘗試仿真大信號（數百千伏）的產(chǎn)生。

 

兩個(gè)電容（與電阻并聯(lián)）決定放大器主極點(diǎn)和壓擺率。目前，宏模型只能處理對稱(chēng)的正負壓擺率，因為對稱(chēng)是最容易仿真的情況。但是，未來(lái)的增強宏模型可能允許仿真對稱(chēng)正負壓擺率之間的一些變化。最后，該級在這兩個(gè)電壓控制電流源上各添加一個(gè)直流分量，構成放大器靜態(tài)電源電流的主要部分。

 

對運算放大器頻率響應的研究表明，在大多數情況下，精確仿真實(shí)際器件在高頻率下的增益和相位變化需要兩個(gè)以上的極點(diǎn)。此外，不同類(lèi)型的運算放大器具有不同數量的極點(diǎn)和零點(diǎn)。為了讓這些不同類(lèi)型的電路都能輕松轉換成兼容SPICE的子電路（而不必每次都從頭開(kāi)始），那么一個(gè)真正的通用模型必須是高度模塊化的，并且具有任意數量（大量）的極點(diǎn)和零點(diǎn)。所以，最終架構使用了所有單個(gè)運算放大器模型都通用的一些基本構建模塊。這些模塊如圖4所示。

 

所有頻率成形模塊在DC條件下具有單位增益，因為每個(gè)電壓控制電流源(VCCS)的gm都等于從VCCS（電壓控制電流源）的每個(gè)節點(diǎn)連接至電源軌的電阻的倒數。這種拓撲結構優(yōu)勢在于，在為一個(gè)特定放大器生成模型時(shí)，可以標注單獨的極點(diǎn)或極零點(diǎn)對。因而可以查看它們各自對放大器的凈頻率響應的影響，這樣極零點(diǎn)調整變得非常容易。因為所有頻率成形模塊在DC條件下都具有單位增益，所以這個(gè)過(guò)程不會(huì )改變模型的DC開(kāi)環(huán)增益。

 

圖4中的共模增益級由兩個(gè)VCCS組成，它們驅動(dòng)兩個(gè)等值電阻，每個(gè)電阻與一個(gè)電感串聯(lián)連接至其中一個(gè)電源軌。電感仿真大部分放大器隨著(zhù)輸入頻率增加而表現出的CMRR的典型衰減。輸入共模電壓（相對于Vh節點(diǎn)）控制電流源。每個(gè)控制電流源的gm都等于相關(guān)電阻值除以DC條件下放大器的CMRR的值的倒數。

 

所以，從輸入共模網(wǎng)絡(luò )到內部共模增益節點(diǎn)的增益等于放大器的CMRR的倒數。（“增益”一詞用在這里并不恰當，因為共模增益的值要遠小于單位增益）。

 

SPICE仿真器的發(fā)展

 

電路仿真器SPICE及其增強版本SPICE2最初是加州大學(xué)伯克利分校在上個(gè)世紀70年代開(kāi)發(fā)出來(lái)的（見(jiàn)參考文獻4）。最初是為了幫助設計工程師在晶體管級分析集成電路（所以這個(gè)首字母縮略詞是表示：Simulation Program with integrated Circuit Emphasis，集成電路模擬的仿真程序）。相比在實(shí)驗室由人力計算，SPICE支持使用計算機評估設計，其速度更快，也更徹底。SPICE迅速流行，很快傳播到系統級設計社區，受到IC設計人員的青睞。

 

初版SPICE是一個(gè)公用程序，僅象征性收取少量費用；但是，許多軟件供應商都意識到需要一個(gè)完全受支持、可以調整和不斷改進(jìn)的商用電路仿真器。這類(lèi)程序的第一個(gè)基于大型機的版本包括Meta-Software的HSpice、NCSS分時(shí)軟件的I-Spice和電子工程軟件的precision。近來(lái)，大部分大型機版本經(jīng)過(guò)調整可用于工作站，還有一些可用于IBM PC和兼容產(chǎn)品。

 

SPICE的首個(gè)PC版本是由MicroSim Corp推出的PSpice。之后陸續推出了其他版本，例如Intusoft推出的IS-Spice。其他公司，包括ADI公司（提供一種名為Saber的行為仿真軟件包）已經(jīng)選擇脫離傳統的SPICE格式，放棄使用“盒裝”電路元件來(lái)構建模型。相反，Saber基于嚴格定義的用一種稱(chēng)為Mast的特定建模語(yǔ)言編寫(xiě)的方程來(lái)控制任何所需電路模型的行為。

 

電感器在共模增益上增加一個(gè)零點(diǎn)，這相當于在共模CMRR上增加一個(gè)極點(diǎn)。共模電壓，在經(jīng)過(guò)擴展和適當的頻率成形之后，按照理論要求輸送回輸入級。這一步通過(guò)將輸入級偏置電壓源變成單位增益電壓控制電壓源來(lái)實(shí)現，其直流分量等于放大器的VOS。

 

圖5中并未完全顯示輸出級的操作。在接收所有適當的頻率成形之后，內部運算放大器輸出信號顯示為以輸出級處理之前的最后一個(gè)節點(diǎn)的Vh為基準的電壓。輸出模塊中的兩個(gè)電壓控制電流源驅動(dòng)兩個(gè)連接至供電軌的等值電阻，就像其他模塊一樣。但是，此時(shí)，兩個(gè)電壓控制電流源的gm的排列方式使它們能夠作為有源電流發(fā)生器。所以，每個(gè)gm源產(chǎn)生的電流恰好足以通過(guò)并行電阻提供所需壓降。

 

當輸出端沒(méi)有負載時(shí)，該模型不會(huì )從任一電源軌吸取電流。所以，它表現得比較像是理想的單位增益B類(lèi)輸出級，且無(wú)交越失真。因為兩個(gè)電阻的值都等于開(kāi)環(huán)輸出電阻的兩倍，所以輸出級看起來(lái)就像是以Vh為基準的電壓源，具有正確的DC輸出電阻。仿真正確的輸出電阻意味著(zhù)DC開(kāi)環(huán)增益會(huì )在放大器加載時(shí)適當降低。

 

模型參數計算

 

以下公式可用于構建改進(jìn)的宏模型，以實(shí)現任何運算放大器仿真。它分別針對每個(gè)可用的構建模塊進(jìn)行計算，并討論了一些電源考量因素。

 

輸入級和增益級計算

 

a. 通用計算

 

參考圖3來(lái)確定此處提到的元件和信號。首先，選擇IEE，其值要略小于放大器的總靜態(tài)電流。為方便起見(jiàn)，可以將IEE設置為1mA、100µA、10µA或1µA，

 

 

其中fp1 =放大器主極點(diǎn)，

 

 

AVOL = 開(kāi)環(huán)直流增益

 

 

fp2 = 第二放大器極點(diǎn)

 

 

T = 27°C

 

 

（兩個(gè)二極管均適用）。

 

您可以將數據手冊中的一些參數直接運用到模型中。這些參數包括：

 

EOS =輸入失調電壓（僅限直流分量）；

IOS = 輸入失調電流；CIN = 輸入電容。

 

b. 雙極性輸入級計算

 

首先，必須評估以下公式，確定是否可以使用新宏模型對討論的運算放大器進(jìn)行建模：

 

 

其中VT = 0.02585V（27°C時(shí)）。

 

如果此方程成立，可以繼續進(jìn)行接下來(lái)的計算。如果不成立，則必須修改模型，使其與特定的運算放大器匹配。

 

 

其中βF為輸入晶體管的正向電流增益，IBIAS為輸入偏置電流。

 

 

其中RID為差分輸入電阻。如果RID不是指定的數據手冊參數，則將R1和R2的值設為5 x 1011Ω。

 

c. JFET輸入級計算

 

如果設計中包含JFET輸入級，則使用柵極至源極截止電壓VTO的默認值-2.000V。另外，將第一級電流源的名稱(chēng)改為ISS。主要計算是確定β，即JFET的增益系數：

 

 

其中ISS為第一級尾電流。

 

為了獲得最大輸出dV/dt，尾電流只能來(lái)自差分對的一側；因此需要差分輸入電壓等于：

 

 

此外，輸入偏置電流由柵極漏極電流和柵極源極漏電流組成。所以，

 

 

其中IBIAS為27℃時(shí)的輸入偏置電流。此外，

 

 

其中RID為差分輸入電阻（一般為1 x 1012Ω。

 

最后，可以將R5和R6的值設置為零，因為JFET輸入放大器通常不需要降級。

 

頻率成形級計算

 

要確認頻率成形級的參數，請參見(jiàn)圖4。在所有三類(lèi)頻率成形級中，為方便起見(jiàn)，將G3和G4設置為A/V的1 x 10-6倍。此外，fZ為零點(diǎn)頻率，fp為極點(diǎn)頻率。 

 

然后，在極零點(diǎn)級，

 

 

在零極點(diǎn)級，

 

 

在極點(diǎn)級，

 

 

共模增益級計算

 

要確認共模增益級的參數，請參見(jiàn)圖4。

 

 

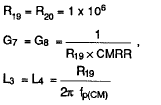
其中，fCM為共模極。

 

輸出級計算

 

要確認輸出級的參數，請參見(jiàn)圖5。二極管D7和D8的擊穿電壓標稱(chēng)值設置為50V。通過(guò)實(shí)驗確定了電感L5的值。ROUT為開(kāi)環(huán)輸出阻抗；VT為0.02585V（27°C時(shí)）；所有二極管的IS均為1 x 10-12A。所以：

 

 

可以通過(guò)以下公式確定圖3中電阻R9和R10的值：

 

 

其中dISY/dVSY表示電源電壓變化引起的電源電流變化。該模型中VCC與VEE之間的總靜態(tài)電流為：

 

 

其中，N為該模型中頻率成形和共模增益級的總數；R一般為1 x 106Ω；此值以及頻率成形級中G源的跨導，可以根據低功耗運算放大器適當調整；

 

IDC是增加至G1和G2源的直流偏移，以補償模型的剩余部分消耗的電流和  的靜態(tài)電流之間的差值

 

但是，這種簡(jiǎn)單的推挽式輸出級存在一個(gè)微妙的問(wèn)題。無(wú)論這個(gè)級是吸電流還是源電流，負載電流總是均勻分布在兩個(gè)電源軌上，而實(shí)際輸出級不會(huì )如此。所以，以源負載電流為例，凈正電源電流的增加幅度只有流入負載中電流的一半。而負電源電流則是減少相同的量。為了補償這種異常，會(huì )強制電流從正電源軌流向負電源軌，數量正好是負載電流的一半。這種校正電流必須始終沿著(zhù)相同的方向流動(dòng)——即使輸出電流的極性相反。

 

圖6：OP-42宏模型遠比Boyle模型復雜，需要更長(cháng)的仿真時(shí)間，但其精度大幅提高

 

列表1：OP-42 SPICE宏模型網(wǎng)絡(luò )列表

OP-42宏模型 © PMI 1990

SUBCKT OP-42 1 2 30 99 50

15.9 MHZ時(shí)的輸入級和極點(diǎn)

 

 

45 HZ時(shí)的第二級和極點(diǎn)

 

 

1.80 MHZ/2.20 MHZ時(shí)的極零點(diǎn)對

 

 

1.80 MHZ/2.20 MHZ時(shí)的極零點(diǎn)對

 

 

53 MHZ時(shí)的極點(diǎn)

 

 

53 MHZ時(shí)的極點(diǎn)

 

 

53 MHZ時(shí)的極點(diǎn)

 

 

100 KHZ時(shí)增益為零的共模增益網(wǎng)絡(luò )

 

 

79.6 MHZ時(shí)的極點(diǎn)

 

 

輸出級

 

 

使用的模型

 

JX PJF模型(BETA=999.3E-6 VTO=-2.000 IS=8E-11)

 

DX模型 D(IS=1E-15)

 

DY模型 D(IS=1 E-15 BV=50)

 

ENDS OP-42

 

因此，圖5中兩個(gè)校正源的作用是在供電軌之間產(chǎn)生一個(gè)等于輸出電流一半的單極性補償電流。在SPICE中，因為難以實(shí)現絕對值VCCS，所以必須具有兩個(gè)線(xiàn)性校正源——一個(gè)校正源對應半個(gè)輸出電流周期。與每個(gè)源串聯(lián)的二極管執行半波整流，

 

齊納二極管確保當電流反向時(shí)，始終為每個(gè)源提供導電路徑。所有這些附加元件最終形成了一個(gè)輸出級模型，其直流行為非常接近實(shí)際電路的行為。

 

為了解決發(fā)射極跟隨器輸出級阻抗隨頻率升高的典型現象，宏模型內置一個(gè)輸出電感，連接在中間輸出節點(diǎn)和實(shí)際宏模型輸出節點(diǎn)之間（參見(jiàn)圖5）?？梢酝ㄟ^(guò)在模型上使用容性負載來(lái)確定這個(gè)電感的值，經(jīng)過(guò)不斷試驗和試錯，直到過(guò)沖量與采用同樣負載的實(shí)際運算放大器極為接近為止。

 

出色的運算放大器宏模型還必須具備短路電流限制特性，在圖5中，通過(guò)使用二極管D3和D4以及電壓源V3和V4，將前一個(gè)頻率成形級的輸出電壓(VF)箝位到中間輸出節點(diǎn)(V0)來(lái)實(shí)現限制。注意，在沒(méi)有負載的情況下，前一級的信號始終等于理想的輸出電壓，并且輸出級就像是具有有限輸出阻抗的電壓源。二極管和電壓源的作用相當于箝位有效輸出電阻上的壓降。通過(guò)適當選擇每個(gè)電壓源，可以獲得所需的輸出限流。

 

由于新結構的主要目標是提高交流精度，因此該模型也必須正確表示共模行為。因此，建模團隊選擇PMI OP-42（JFET輸入運算放大器）作為第一個(gè)實(shí)驗對象，主要是因為Boyle模型無(wú)法正常仿真JFET輸入級。雖然在測試整個(gè)模型之前，該團隊必須計算出與JFET輸入級有關(guān)的所有方程，但之后發(fā)現，從數學(xué)角度處理這個(gè)級相當容易，并不妨礙最終的宏模型結構開(kāi)發(fā)。

 

圖7：以單位增益、反相配置連接OP-42時(shí)，增益響應在6MHz左右有一個(gè)小高峰；2MHz之后，相位偏移急劇增加。

 

圖8：采用新的宏模型，OP-42的仿真增益響應(a)與實(shí)際器件非常相似，在4MHz有一個(gè)小峰值。相位響應(b)非常不錯。這條曲線(xiàn)與實(shí)際器件的曲線(xiàn)非常接近。

 

圖9：OP-42的Boyle模型(a)在4MHz時(shí)，沒(méi)有顯示實(shí)際器件所具備的幅度峰值特性。相位響應(b)也不是很準確，特別是在超過(guò)10MHz的區域。

 

圖10：具有430pF電容負載的OP-42在500kHz、200mV峰值方波的驅動(dòng)下顯示過(guò)沖和欠沖

 

圖6顯示隨之得出的結果。實(shí)際OP-42具有約10MHz的增益帶寬乘積，以及50V/µs的對稱(chēng)壓擺率。從該放大器的CMRR與頻率關(guān)系曲線(xiàn)可以看出，該模型的共模增益級需要一個(gè)零點(diǎn)（約100kHz處）。

 

列表1所示為OP-42宏模型的網(wǎng)絡(luò )列表，它有8個(gè)極點(diǎn)、2個(gè)零點(diǎn)，以及在共模增益級的100kHz處的一個(gè)零點(diǎn)。即使是一個(gè)相對穩定的放大器模型也需要這些極點(diǎn)和零點(diǎn)，以便準確地模擬實(shí)際器件在高頻率下的增益和相位行為。

 

查看網(wǎng)絡(luò )列表的輸出級部分可知，開(kāi)環(huán)輸出電阻為45Ω。與輸出端口串聯(lián)的250nH電感可以補償高頻率下有效開(kāi)環(huán)輸出阻抗的上升。由二極管D3和D4以及電壓源V3和V4組成的限流網(wǎng)絡(luò )將最大輸出電流箝位在約±30mA。

 

仿真精度比較

 

圖7顯示作為反相單位增益放大器連接的實(shí)際OP-42的增益和相位響應，該放大器具有1kΩ輸入和反饋電阻，采用±15V電源供電。在閉環(huán)增益曲線(xiàn)上，可以看到一個(gè)小峰值（約2dB），在超過(guò)2MHz之后，相位偏移急劇增加。圖8a和圖8b顯示在相同條件下，新OP-42宏模型的增益和相位響應。增益響應顯示與實(shí)際電路具有相同的閉環(huán)峰值；相位響應與實(shí)際器件的相位響應幾乎完全一樣，至少達到10MHz。

 

圖9a和9b顯示采用Boyle模型時(shí)的輸出曲線(xiàn)，從中可以明顯看出Boyle模型在響應精度方面的缺陷。增益響應未出現2dB峰值，表明急劇滾降，在超過(guò)10MHz之后，結果非常不準確。Boyle模型的相位響應與實(shí)際電路的響應相去甚遠。OP-42宏模型采用多個(gè)極零點(diǎn)補碼，可以更準確地仿真實(shí)際電路的交流響應。

 

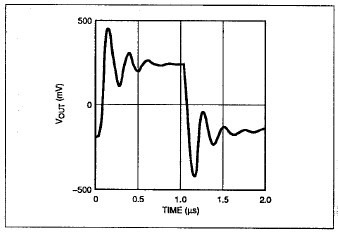
圖11：采用新的宏模型仿真OP-42（采用430pF容性負載）的結果顯示，該模型的輸出級具有對稱(chēng)性

 

圖12：采用Boyle模型仿真OP-42時(shí)，仿真了大約等量的過(guò)沖，但其振鈴頻率過(guò)低

 

圖10顯示在430pF容性負載下，測量的反相單位增益OP-42放大器的瞬態(tài)響應。對于400mVp-p輸入信號，大約有75%的過(guò)沖和100%的欠沖。新的宏模型仿真結果（參見(jiàn)圖11）顯示大約115%的過(guò)沖和欠沖。這個(gè)仿真值與波形負半部的實(shí)際值相當接近，但與正半部的實(shí)際值不同。對于這種異常，給出的解釋是：盡管新的宏模型的輸出級完全對稱(chēng)，但所建模的運算放大器可能并非如此。OP-42實(shí)際上具有不對稱(chēng)、完全由NPN晶體管組成的輸出級。所以，高頻開(kāi)環(huán)響應是可變的，具體取決于輸出級是吸電流還是源電流。

 

Boyle配置也將運算放大器的輸出級建模為完全對稱(chēng)的電壓源，如圖12所示，它在輸出波形負半部的欠沖仿真并不正確。它在正半部的仿真與實(shí)際電路非常接近，但是振鈴頻率低于實(shí)際電路。

 

圖13：除了多了一個(gè)增益級之外，OP-61的模型示意圖與OP-42類(lèi)似

 

列表2：OP-61 SPICE宏模型網(wǎng)絡(luò )列表

OP-61宏模型 © PMI 1989

SUBCKT OP-61 1 2 34 99 50

300 MHZ時(shí)的輸入級和極點(diǎn)

 

 

第一個(gè)增益級

 

 

2.5KHZ時(shí)的第二增益級和極點(diǎn)

 

 

4MHZ / 8MHZ時(shí)的極零點(diǎn)對

 

 

85MHZ / 300MHZ時(shí)的零極點(diǎn)對

 

 

40MHZ時(shí)的極點(diǎn)

 

 

200MHZ時(shí)的極點(diǎn)

 

 

200MHZ時(shí)的極點(diǎn)

 

 

200MHZ時(shí)的極點(diǎn)

 

 

40 KHZ時(shí)增益為零的共模增益網(wǎng)絡(luò )

 

 

300MHZ時(shí)的極點(diǎn)

 

 

輸出級

 

 

使用的模型

 

QX NPN模型(BF=1250)

DX模型 D(IS=1E-15)

DY模型 D(IS=1E-15 BV = 50)

ENDS OP-61

 

Boyle方法本身不支持對非對稱(chēng)輸出級行為建模，很遺憾，這種新的宏模型也是如此。但是，這個(gè)缺陷是可以解決的。如果在生成模型的過(guò)程中發(fā)現過(guò)沖值與欠沖值不同，那么在輸出電感相關(guān)計算中應使用兩個(gè)值中較大的一個(gè)。然后，在容性負載下，該電感值將會(huì )產(chǎn)生最差情況下的過(guò)沖和欠沖結果。

 

執行時(shí)間比較

 

假設宏模型不存在收斂問(wèn)題，那么SPICE進(jìn)行操作點(diǎn)計算或生成直流轉換曲線(xiàn)所需的時(shí)間很大程度上取決于網(wǎng)絡(luò )列表中指定的電路元件數量。因此，新的OP-42宏模型的速度幾乎比Boyle模型慢一半，需要進(jìn)行2.27次迭代，才能得出最終的解決方案。對于交流分析案例，情況也是這樣，新的宏模型的運行時(shí)間幾乎是Boyle宏模型的兩倍。但是，在仿真交流響應時(shí)，這兩種模型需要的迭代次數基本是相同的。

 

由于所涉因素很多，很難評估瞬態(tài)分析需要多大的計算量。特別是，新的宏模型會(huì )展示比Boyle模型更多的細節。所以，仿真器必須使用更精細的時(shí)間步長(cháng)，相應地執行更多的計算。但是，模型中大量的理想元件使得模型具有很好的收斂性能。所以，有時(shí)可以通過(guò)在單個(gè)時(shí)間步長(cháng)內進(jìn)行更多次迭代來(lái)加快分析速度，這樣，仿真器可以保持粗略的時(shí)間步長(cháng)，并減少回溯次數。

 

大多數SPICE仿真器將瞬變迭代次數默認為10。您可以在.OPTIONS部分將ITL4設置為一個(gè)更大的數值（比如40），以覆蓋這個(gè)默認值。此外，將RELTOL放寬到0.01（默認值通常為0.001），通過(guò)略微降低準確性也可加快運行時(shí)間。這種降低是可行的，因為宏模型本身也只是一種近似法。但是，請注意，圖11和圖12是在RELTOL設置為0.001而不是0.01時(shí)生成的，所以曲線(xiàn)會(huì )更為準確。另一種加快瞬態(tài)分析速度的方法是使用GEAR積分，而不是梯形積分；但是，使用這種積分得出結果的振蕩幅度要比實(shí)際結果低得多。

 

RELTOL使用0.01，ITL4和梯形積分使用40，OP-42宏模型的瞬變運行速度比Boyle慢3.64倍，且需要2.15倍迭代。仿真速度雖然大幅降低，但是可以接受，并且精度大大提高，足以抵消這種降低。

 

OP-61宏模型

 

OP-61是一種雙極輸入寬帶精密運算放大器，典型的增益帶寬積為200MHz（測試頻率為1 MHz時(shí)），壓擺率為40V/µs。圖13所示的這種器件的模型比OP-42的模型稍微復雜一點(diǎn)。OP-61的共模抑制在比OP-42的CMRR低的頻率下開(kāi)始滾降，但在1MHz時(shí)，其值仍然非?？捎^(guān)，為80dB。網(wǎng)絡(luò )列表（參見(jiàn)列表2）表明OP-61模型需要9個(gè)極點(diǎn)和2個(gè)零點(diǎn)來(lái)模擬開(kāi)環(huán)頻率響應，并且共模增益在40kHz時(shí)為零。

 

注意，這個(gè)模型在差分輸入級和主增益級（參見(jiàn)圖13c）之間有一個(gè)額外的增益級（圖13中的級b），可以生成放大器主極點(diǎn)。這個(gè)特殊的模型需要額外的增益級，因為OP-61不能滿(mǎn)足極限方程要求，該方程涉及雙極性輸入級的壓擺率、開(kāi)環(huán)增益和主極點(diǎn)頻率（參見(jiàn)框1）。OP-61模型需要100dB開(kāi)環(huán)增益和40V/µs壓擺率，但其增益帶寬積（以及由此得出的主極點(diǎn)頻率）太高，無(wú)法由單個(gè)級生成所有開(kāi)環(huán)電壓增益。

 

所以，該模型使用兩個(gè)增益級，共同提供所需的100dB增益。第一個(gè)增益級的增益為200；第二個(gè)為500。必須對第一個(gè)增益級箝位，以限制施加給第二個(gè)增益級中電壓控制電流源的最大驅動(dòng)電壓。這個(gè)箝位操作會(huì )限制傳遞給補償電容C5和C6的峰值電流，從而限制第二個(gè)增益級的最大dV/dt。

 

因為輸入級的最大差分輸出電壓僅為51.6mV，所以第一個(gè)增益級必須提供較大增益。為了便于對電壓源和二極管進(jìn)行箝位，需要一個(gè)更大的電壓。第一個(gè)增益級的200增益在擺動(dòng)期間可以產(chǎn)生相對于Vh的±10.32V無(wú)阻尼電壓，但是無(wú)論使用哪個(gè)供電軌，箝位電路都會(huì )將此值限制為約±5.0V。這種配置支持進(jìn)行可靠箝位，即使電源電壓低至±4.4V，這也導致所需壓擺率為40V/µs。

 

圖14：將一個(gè)實(shí)際OP-61連接為反相放大器，增益為10時(shí)，增益響應在10MHz時(shí)顯示達到3dB峰值。

 

圖15：OP-61宏模型的仿真增益(a)顯示了在10MHz時(shí)的正確峰值。此外，它在40MHz時(shí)的相位響應(b)與實(shí)際器件的響應僅偏差10°。

 

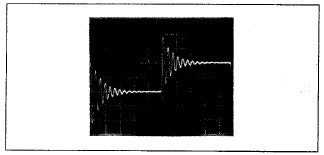
圖16：實(shí)際OP-61連接為反相放大器，且增益為10，容性負載為207pF時(shí)，其瞬態(tài)響應不太對稱(chēng)。輸入信號為500kHz方波，峰值幅度為10mV。垂直標度為0.1 V/div，水平標度為0.2µs/div。

 

圖17：OP-61宏模型仿真的瞬態(tài)響應非常接近實(shí)際器件的瞬態(tài)響應

 

仿真精度比較

 

圖14顯示了配置為反相放大器、增益為10的實(shí)際OP-61的增益和相位響應測量值。其中使用了一個(gè)1kΩ反饋電阻、一個(gè)100Ω輸入電阻和±15V電源。在10MHz范圍內，振幅響應出現約3dB的峰值，在10MHz以上，相位偏移急劇增加。對于這些響應，新的宏模型（參見(jiàn)圖15a和15b）的測量值與OP-61非常一致。增益曲線(xiàn)顯示，在稍高于10MHz的位置，出現了所需的增益峰值（稍微超出2dB）。相位響應精度也非常不錯；在40MHz時(shí)，誤差只有10°左右，可能在試驗板由于寄生電容和其他物理效應導致的偏差范圍內。因此，這個(gè)新的宏模型是一個(gè)可以預測OP-61性能的有用工具，甚至可以在評估試驗板之前進(jìn)行預測。

 

圖16顯示了OP-61的瞬態(tài)響應，看起來(lái)非常不穩定，但該器件正在驅動(dòng)207pF容性負載。該波形顯示過(guò)沖量和欠沖量之間存在一些不對稱(chēng)性（180%對比220%），但是OP-61和OP-42一樣，并沒(méi)有完全平衡的輸出級結構。所選的輸出電感（模型中的L5）在很大程度上決定了仿真的瞬態(tài)響應與實(shí)際響應之間的相似程度。事實(shí)上，圖17所示的仿真產(chǎn)生了對稱(chēng)的過(guò)沖和欠沖（約150%），與圖16相比稍低，但其振鈴頻率則稍高。這種差異對用戶(hù)來(lái)說(shuō)并不太重要。但是，如果這很重要，可以稍微增大輸出電感的值，使仿真響應更接近實(shí)際器件響應。

通過(guò)與OP-42（沒(méi)有OP-61的Boyle模型）比較，您可以大致了解新OP-61模型的性能。在計算直流偏置點(diǎn)時(shí)，OP-61宏模型比OP-42宏模型更快。但是，進(jìn)行交流響應仿真時(shí)，OP-61宏模型則比OP-42宏模型慢1.18倍。

 

進(jìn)行瞬態(tài)響應仿真時(shí)，OP-61宏模型所花的時(shí)間是OP-42宏模型的1.76倍，迭代次數是OP-42的1.56倍。在這方面，您應該記住，瞬態(tài)運行的仿真時(shí)間隨著(zhù)輸出振蕩的加劇而增加。所以，直接比較OP-42和OP-61的執行時(shí)間并不公平，因為OP-42的響應比OP-61更平緩。

 

仿真目標在不斷改變

 

計算機模型用于對一些物理現象進(jìn)行準確建模；現象越復雜，計算機執行必要計算所需的時(shí)間就越長(cháng)。Boyle運算放大器模型的目標是減少需要仿真的非線(xiàn)性元件的數量，從而將運行時(shí)間縮短至可接受的水平。Boyle模型在建立時(shí)并未考慮到最終準確性，但它可以正確預測運算放大器的低頻性能，對于當時(shí)的低性能器件來(lái)說(shuō)，結果是令人滿(mǎn)意的。

 

但是如今，對更高性能的需求日益增長(cháng)，如果可以準確預測新器件的性能，則可以幫助避免設計錯誤，以免在生產(chǎn)階段因糾正這些錯誤耗費大量成本。所以，準確的高頻性能建模至關(guān)重要，在這一領(lǐng)域，Boyle模型無(wú)法滿(mǎn)足需求。本文所描述的經(jīng)過(guò)改進(jìn)的運算放大器宏模型不僅能比Boyle模型更準確地仿真運算放大器的高頻響應和瞬態(tài)行為，還不會(huì )耗費過(guò)多的CPU時(shí)間。如今，擁有了強大的桌面工作站，建模的重點(diǎn)是提高仿真精度，而不是縮短執行時(shí)間。所以，新的宏模型提供了良好的折衷方案。

 

這個(gè)新的宏模型的最大限制因素在于：為了保證SPICE的兼容性，該模型必須以包含實(shí)際電路元件的網(wǎng)絡(luò )列表的形式編寫(xiě)。一些新仿真器（如ADI公司的Saber）允許您用專(zhuān)門(mén)的編程語(yǔ)言來(lái)定義模型，無(wú)需采用電路類(lèi)型架構。Saber建模語(yǔ)言稱(chēng)為Mast，與C語(yǔ)言非常類(lèi)似，可以有效管理內部變量。例如，允許完全用數學(xué)方法來(lái)描述新的宏模型的輸出級。Saber模型不需要SPICE模型用來(lái)對輸出級電流實(shí)施校正的所有二極管和額外源。輸出級的定義方程會(huì )直接考慮從模型輸出端獲取的任何負載電流。在不久的將來(lái)，新的宏模型很可能會(huì )在Saber中實(shí)現。

 

參考文獻

 

1. Boyle, Graeme R., et al, "Macromodeling of Integrated Circuit Operational Amplifiers," IEEE Journal of Solid State Circuits, Vol. sc-9, no. 6, December, 1974.

2. Gray, Paul R. and Robert G. Meyer, Analysis and Design of Analog Integrated Circuits, John Wiley & Sons, 1977, pp 159-161.

3. ibid, pp 175-177.

4. Laurence W. Nagel，“SPICE2：A Computer Program to Simulate Semiconductor Circuits," U.C.Berkeley Memorandum No. M520, May, 1975.

 

 

推薦閱讀：