柵瓣簡(jiǎn)介

 

到目前為止，我們只見(jiàn)過(guò)元件間隔為d = λ/2這種情況。圖1開(kāi)始說(shuō)明為什么λ/2的元件間隔在相控陣中如此常見(jiàn)。圖中共顯示兩種情況。首先，是藍色線(xiàn)條，重復顯示第1部分圖11中的30°圖。接下來(lái)，d/λ間隔增加到0.7，以顯示天線(xiàn)方向如何變化。注意，隨著(zhù)間隔增加，波束寬度減小，這是一個(gè)積極現象。零值間隔減小使它們的距離更接近，這也可以接受。但是現在出現了第二個(gè)角度，在本例中為–70°,在該角度下出現了全陣列增益。這是最為不利的情況。這種天線(xiàn)增益復制被定義為一個(gè)柵瓣，可以被認為是空間混疊。

 

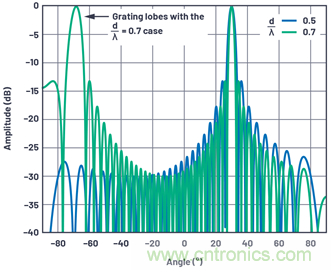
圖1.在兩種不同的d/λ間隔下，32元件線(xiàn)性陣列的標準化陣列因子。

 

采樣系統的類(lèi)比

 

為實(shí)現柵瓣可視化，可以將其類(lèi)比為采樣系統中的混疊現象。在模數轉換器(ADC)中，接收器結構通常會(huì )對頻率進(jìn)行欠采樣。欠采樣包括有意降低采樣率(fS)，通過(guò)采樣過(guò)程將高于fS/2的頻率（較高的奈奎斯特區）轉換為第一個(gè)奈奎斯特區的混疊。這使得這些較高頻率看起來(lái)似乎在A(yíng)DC輸出端為較低頻率。

 

可以考慮在相控陣中采用類(lèi)似的類(lèi)比方法，在該陣列中，由元件對波前進(jìn)行空間采樣。如果我們建議為了避免混疊，對每個(gè)波長(cháng)實(shí)施兩次采樣（即元件），那么奈奎斯特準則可以擴展應用到空間區域。因此，如果元件間隔大于λ/2，我們可以考慮這種空間混疊。

 

計算柵瓣出現的位置

 

但是這些空間混疊（柵瓣）會(huì )出現在哪里？在第1部分中，我們展示了整個(gè)陣列中元件的相移與波束角度之間的函數關(guān)系。

 

 

 

反過(guò)來(lái)，我們可以根據與相移的函數關(guān)系來(lái)計算波束角度。

 

 

arcsin函數只產(chǎn)生-1和+1之間的實(shí)數解。在這些范圍之外，無(wú)法得到實(shí)數解，電子數據表軟件中會(huì )出現“#NUM!”。還要注意，方程2中的相位呈周期性，每隔2π重復一次。所以，我們可以使用(m × 2π + ?Φ)取代波束轉向公式中的?Φ，進(jìn)而得出公式3。

 

 

其中m = 0、±1、±2…

 

為了避免柵瓣，我們的目標是獲得單一實(shí)數解。從數學(xué)上講，這通過(guò)使下式成立來(lái)實(shí)現

 

 

如果我們這樣做，那么所有的空間圖像（即m =±1、±2等）將產(chǎn)生非實(shí)數arcsin結果，我們可以忽略它們。但如果我們不能這樣做，那么某些m > 0的值會(huì )產(chǎn)生實(shí)數arcsin結果，那么我們會(huì )得出多個(gè)解：柵瓣。

 

圖2.arcsin函數在柵瓣中的應用。

 

d > λ和λ = 0°的柵瓣

 

讓我們嘗試通過(guò)一些示例來(lái)更好地說(shuō)明這一點(diǎn)。首先，考慮機械軸線(xiàn)校準示例，其中θ = 0，所以?Φ = 0。然后，將公式3簡(jiǎn)化為公式5。

 

 

通過(guò)這種簡(jiǎn)化，可以明顯看出，如果λ/d > 1，那么只有當m = 0，才可以得出在–1和+1之間的參數。這個(gè)參數就是0，且arcsin(0) = 0°，也就是機械軸線(xiàn)校準角度。這就是我們期望獲得的結果。此外，m ≥ 1時(shí)，arcsin參數會(huì )非常大(>1)，不會(huì )得出實(shí)數結果。我們可以看到，θ = 0和d < λ時(shí)，沒(méi)有柵瓣。

 

但是，如果d > λ（使得λ/d < 1），則會(huì )存在多個(gè)解和柵瓣。例如，如果λ/d = 0.66（即d = 1.5λ），則m = 0和m = ±1時(shí)存在arcsin實(shí)數解。m = ±1是第二個(gè)解，是所需信號的空間混疊。因此，我們會(huì )看到三個(gè)主瓣，分別位于arcsin(0×0.66)、arcsin(1×0.66)和arcsin(-1×0.66)，每個(gè)的振幅都大約相等。如果用度數表示，這些角度為0°和±41.3°。事實(shí)上，這就是圖3中的陣列因子圖所示的內容。

 

圖3.d/λ = 1.5、N = 8時(shí)，軸線(xiàn)校準的陣列因子。

 

λ/2 < d < λ時(shí)的柵瓣

 

在簡(jiǎn)化柵瓣方程（方程5）時(shí)，我們選擇只看機械軸線(xiàn)校準(?Φ= 0)。我們還看到，在機械軸線(xiàn)校準時(shí)，d < λ時(shí)不會(huì )出現柵瓣。但是從采樣理論類(lèi)比中，我們知道，當間隔大于λ/2時(shí)，會(huì )出現一些類(lèi)型的柵瓣。所以，當λ/2 < d < λ時(shí)，柵瓣在什么位置？

 

首先，回顧一下在第1部分的圖4中，相位是如何隨轉向角度變化的。我們看到，當主瓣偏離機械軸線(xiàn)校準時(shí)，?Φ的范圍為0至±π。因此，

 

 

的范圍為

 

 

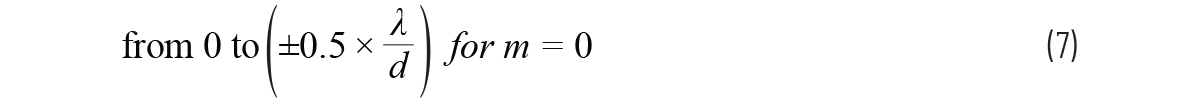
|m|≥1時(shí)，其值則超出該范圍

 

 

如果我們想要在所有|m| ≥ 1的情況下，保持整個(gè)arcsin參數> 1，則會(huì )限制最小可允許的λ/d?？紤]兩種情況：

 

●   如果λ/d ≥ 2（即d ≤ λ/2），則無(wú)論m的值為多少，都不會(huì )出現多個(gè)解。m > 0的所有解都會(huì )導致arcsin參數 > 1。這是唯一避免水平方向出現柵瓣的方法。

●   但是，如果我們有意將?Φ限制為小于±π，那么我們可以接受較小的λ/d，且不會(huì )出現柵瓣。減小?Φ的范圍意味著(zhù)減小陣列的最大轉向角度。這是一種有趣的權衡，將在下一節中探討。

 

元件間隔考慮

 

元件間隔是否應該始終小于λ/2？并非如此！這就是天線(xiàn)設計人員需要作出的考慮和權衡。如果波束完全被轉到水平方向，且θ = ±90°，則需要元件間隔為λ/2（如果可見(jiàn)的半圓內不允許出現柵瓣）。但在實(shí)際操作中，可實(shí)現的最大轉向角度總是小于90°。這是由于元件因子，以及在大轉向角度下的其他降低引起的。

 

從圖2所示的arcsin圖中，我們可以看出，如果y軸θ限制為減小的限值，則柵瓣只在不會(huì )使用的掃描角度下出現。對于給定的元件間隔(dmax)來(lái)說(shuō)，這種減小的限值(θmax)是多少？我們之前說(shuō)過(guò)，我們的目標是使下式成立

 

 

我們可以用它來(lái)計算第一個(gè)柵瓣(m =±1)出現的位置?，F在使用第1部分用于?Φ的公式1，得出：

 

 

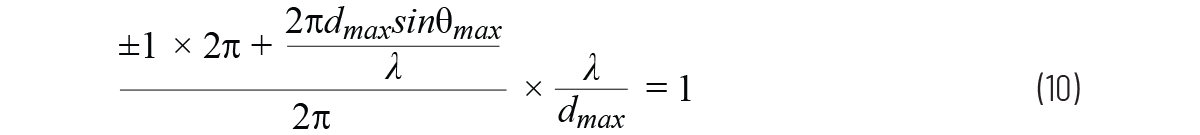
可以簡(jiǎn)化為

 

 

然后得出dmax

 

 

該dmax 是在減小的掃描角度(θmax)下沒(méi)有柵瓣的條件，其中θmax 小于π/2 (90°)。例如，如果信號頻率為10 GHz，我們需要在沒(méi)有柵瓣的情況下轉向±50°，則最大元件間隔為：

 

 

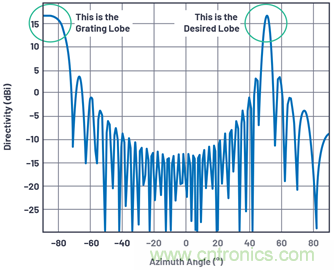
圖4.θ = 50°、N = 32、d = 17 mm且Φ = 10 GHz時(shí)，柵瓣開(kāi)始在水平方向出現。

 

通過(guò)限制最大掃描角度，可以自由地擴展元件間隔，增加每個(gè)通道的物理尺寸，以及擴展給定數量的元件的孔徑。例如，可以利用這個(gè)現象，為天線(xiàn)分配相當狹窄的預定義方向。元件增益可以增大，以在預先定義的方向上提供方向性，元件間隔也可以增大，以實(shí)現更大孔徑。這兩種方法都能在較窄的波束角度下獲得較大的整體天線(xiàn)增益。

 

注意，方程3表示最大間隔為一個(gè)波長(cháng)，即使在零轉向角度下也是如此。在一些情況下，如果柵瓣不出現在可見(jiàn)半圓內即可。以地球同步衛星為例，會(huì )以機械軸線(xiàn)校準為中心，按9°的轉向角度覆蓋整個(gè)地球。在這種情況下，只要柵瓣不落在地球表面就可以。因此，元件間隔可以達到幾個(gè)波長(cháng)，使得波束寬度更窄。

 

還有一些值得注意的天線(xiàn)結構，試圖通過(guò)形成不一致的元件間隔來(lái)克服柵瓣問(wèn)題。這些被歸類(lèi)為非周期陣列，以螺旋陣列為例。由于機械天線(xiàn)構造的原因，我們可能希望有一個(gè)通用的可以擴展為更大陣列的構建模塊，但是，這會(huì )形成一致的陣列，會(huì )受所述的柵瓣條件影響。

 

波束斜視

 

在第1部分中，我們開(kāi)頭描述了在波峰接近元件陣列時(shí)，如何基于相對于軸線(xiàn)校準的波峰角度θ在元件之間出現時(shí)間延遲。對于單一頻率，可以用相移代替時(shí)間延遲來(lái)實(shí)現波束轉向。這種方法適用于窄帶波形，但對于通過(guò)相移產(chǎn)生波束轉向的寬帶波形，波束可能轉移方向（與頻率呈函數關(guān)系）。如果我們記得時(shí)間延遲是線(xiàn)性相移與頻率之間的關(guān)系，則可以直觀(guān)地解釋。所以，對于給定的波束方向，要求相移隨頻率變化?；蛘呦喾?，對于給定的相移，波束方向隨頻率變化。波束角度隨頻率變化的狀況，被稱(chēng)為波束斜視。

 

還考慮到在軸線(xiàn)校準位置θ = 0時(shí)，沒(méi)有跨元件的相移，因此不會(huì )產(chǎn)生任何波束斜視。因此，波束斜視的量必須與角度θ和頻率變化呈函數關(guān)系。圖5顯示一個(gè)X頻段示例。在本例中，中心頻率為10 GHz，調制帶寬為2 GHz，且很顯然波束隨頻率和初始波束角度的變化而改變方向。

 

圖5.32元件線(xiàn)性陣在元件間隔為λ/2時(shí)，在X頻段上的波束斜視示例。

 

波束斜視可以直接計算。使用公式1和公式2，可以計算得出波束方向偏差和波束斜視

 

 

此公式如圖6所示。在圖6中，顯示的f/f0比率是有意的。前一個(gè)方程的倒數(f0/f)提供了一種更容易的方法，可以更直觀(guān)地表示相對于中心頻率的變化。

 

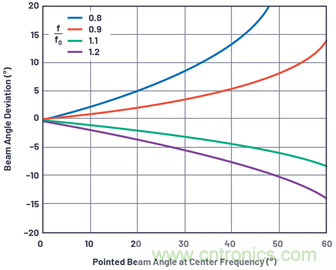
圖6.幾種頻率偏差下的波束斜視和波束角度。

 

關(guān)于波束斜視的幾點(diǎn)觀(guān)察發(fā)現：

 

●   波束角度與頻率的偏差隨著(zhù)波束角度偏離軸線(xiàn)校準的角度增大而增大。

●   低于中心頻率的頻率比高于中心頻率的頻率產(chǎn)生更大的偏差。

●   低于中心頻率的頻率會(huì )使波束更加遠離軸線(xiàn)校準。

 

波束斜視考慮

 

波束斜視，即轉向角度與頻率的偏差，是由相移來(lái)實(shí)現時(shí)間延遲造成的。用真實(shí)時(shí)間延遲單元來(lái)執行波束轉向則不會(huì )出現此問(wèn)題。

 

既然波束斜視問(wèn)題如此明顯，為什么還有人使用移相器，而不是時(shí)間延遲單元呢？一般而言，這歸因于設計簡(jiǎn)單，以及移相器和時(shí)間延遲單元的IC可用性。時(shí)間延遲以某些傳輸線(xiàn)的形式實(shí)現，所需的總延遲時(shí)間與孔徑大小呈函數關(guān)系。到目前為止，大多數可用的模擬波束成型IC都是基于相移，但也出現了一些真實(shí)時(shí)間延遲IC系列，它們在相控陣中更加常見(jiàn)。

 

在數字波束成型中，真實(shí)時(shí)間延遲可以采用DSP邏輯和數字波束成型算法實(shí)現。因此，對于每個(gè)元件都數字化的相控陣架構，它本身就可以解決波束斜視問(wèn)題，并提供最高的編程靈活性。但是，這種解決方案的功能、尺寸和成本都會(huì )造成問(wèn)題。

 

在混合波束成型中，子陣采用模擬波束成型，全陣采用數字波束成型。這可以提供一些值得考慮的波束斜視減少。波束斜視只受子陣影響，子陣的波束寬度更寬，因此對波束角度偏差的容忍度更大。因此，只要子陣的波束斜視是可容忍的，即可在后接真實(shí)時(shí)間延遲（數字波束成型）的子陣內采用帶移相器的混合波束成型結構。

 

總結

 

以上就是有關(guān)相控陣天線(xiàn)方向圖三部分中的第2部分內容。在第1部分，我們介紹了波束指向和陣列因子。在第2部分，我們討論柵瓣和波束斜視的缺點(diǎn)。在第3部分，我們將討論如何通過(guò)天線(xiàn)變窄縮小旁瓣，并讓您深入了解移相器量化誤差。

 

參考電路

 

Balanis, Constantine A. 天線(xiàn)理論：分析與設計，第3版。Wiley-Interscience，2005年。

 

Longbrake, Matthew. 用于雷達的真實(shí)時(shí)間延遲波束控制。2012年度IEEE全國航空與電子學(xué)會(huì )議(NAECON)，IEEE，2012年。

 

Mailloux, Robert J. 相控陣天線(xiàn)手冊，第2版。Artech House，2005年。

 

O’Donnell, Robert M. “雷達系統工程：簡(jiǎn)介。”IEEE，2012年6月。

 

Skolnik，Merrill.雷達手冊，第3版。 McGraw Hill2008年。

 

 

推薦閱讀：