【導讀】人類(lèi)在無(wú)線(xiàn)通信的實(shí)踐過(guò)程中使用信號調制的方式來(lái)將傳遞的信號的頻譜搬移到高頻,通過(guò)天線(xiàn)完成電磁波的發(fā)送與接收。這種信號調制方式作為信號頻譜分析的應用,也是信號與系統課程中的重要內容。

▲ 無(wú)線(xiàn)通訊方式及其天線(xiàn)
本文對信號幅度調制和解調進(jìn)行討論。通過(guò)公式、波形、頻譜分析對幅度調制中的混疊現象進(jìn)行描述。
幅度調制
信號調制中,幅度調制形式簡(jiǎn)單,應用廣泛。在形式可以描述成信號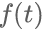 與載波信號
與載波信號 的乘積關(guān)系。在實(shí)際工程中,載波信號的頻率
的乘積關(guān)系。在實(shí)際工程中,載波信號的頻率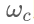 通常遠大于信號
通常遠大于信號 的最高頻率。后期通過(guò)同步解調方式,可以從調制信號中恢復出原來(lái)的信號。
的最高頻率。后期通過(guò)同步解調方式,可以從調制信號中恢復出原來(lái)的信號。
下面公式描述了幅度調制(載波抑制調幅)的過(guò)程:
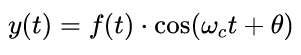
實(shí)現的系統框圖顯示如下:

▲ 信號幅度調制的系統框圖
下面通過(guò)波形顯示了幅度正弦調制的過(guò)程。其中信號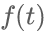 的頻率為1kHz,載波的頻率為30kHz。這樣選擇只是為了能夠從波形上還可以看出兩個(gè)信號的波形。實(shí)際中往往載波的頻譜
的頻率為1kHz,載波的頻率為30kHz。這樣選擇只是為了能夠從波形上還可以看出兩個(gè)信號的波形。實(shí)際中往往載波的頻譜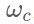 比調制信號
比調制信號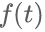 的頻率高出兩三個(gè)數量級以上。
的頻率高出兩三個(gè)數量級以上。
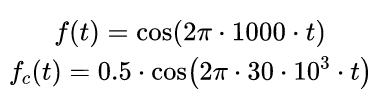

▲ 載波信號與低頻調制信號
下圖顯示了信號 與載波信號
與載波信號 相乘之后的調幅波形。
相乘之后的調幅波形。
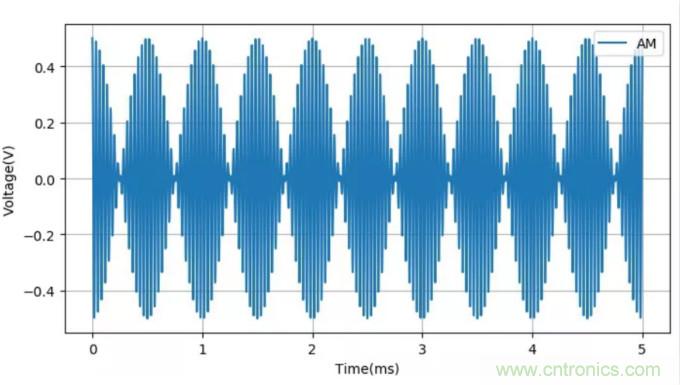
▲ 幅度調制信號
幅度調制后的信號頻譜是原來(lái)信號的頻譜分別左右搬移到載波頻率附近的位置,形成高頻信號。下面顯示了前面正弦信號調制后的頻譜。

▲ 載波抑制幅度調制信號的頻譜
下面顯示了對高斯信號調制后的信號波形:
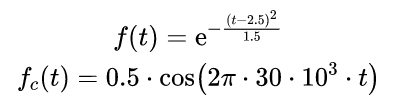
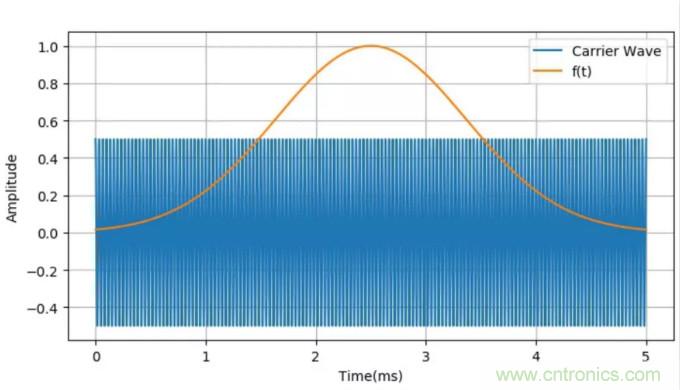
▲ 調制信號與載波信號
高斯信號條幅后的波形如下圖所示。它對應的頻譜與前面正弦波調制后的頻譜相比只是將原來(lái)的一對沖激頻譜改成了高斯信號頻譜。這是由于高斯信號的傅里葉變換也是高斯信號。
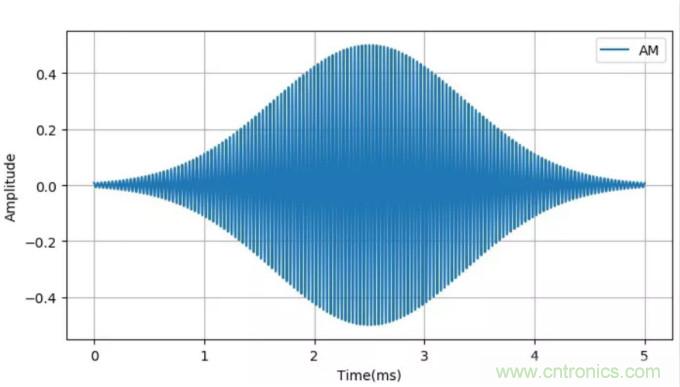
▲ 高斯信號調制后的波形

▲ 高斯信號調制信號頻譜示意圖
同步解調
相比與普通調幅信號,這種載波抑制的調幅需要使用同步檢波的方式來(lái)解調。具體過(guò)程通過(guò)數學(xué)描述如下:

將調幅波形再乘以載波信號,相當于再幅度調制。在生成信號中包括兩個(gè)成分,一個(gè)是信號本身 ,幅度降低了一半;另一個(gè)是信號與兩倍的載頻波形的乘積。后面再通過(guò)一個(gè)低通濾波器便可以將調制信號
,幅度降低了一半;另一個(gè)是信號與兩倍的載頻波形的乘積。后面再通過(guò)一個(gè)低通濾波器便可以將調制信號 進(jìn)行恢復。
進(jìn)行恢復。
下圖顯示了同步解調的過(guò)程以及各部分的波形。
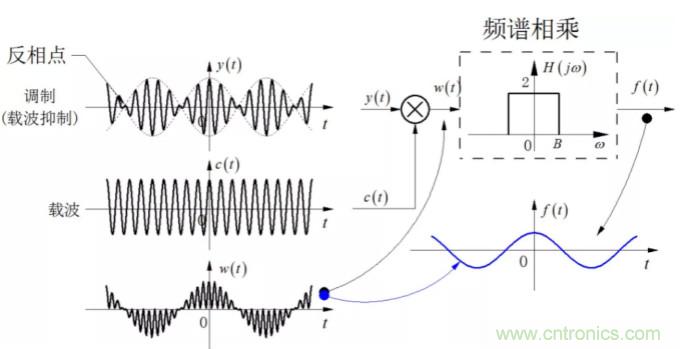
▲ 同步解調的過(guò)程波形圖
對于前面給出的實(shí)驗波形,下面繪制出了信號乘以載波之后的波形??梢钥闯?,其中的低頻分量就是被調制的信號。
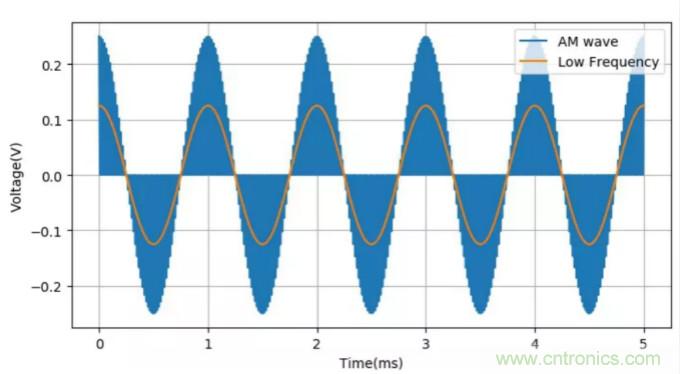
▲ 調幅信號乘以載波信號以及其中的低頻信號
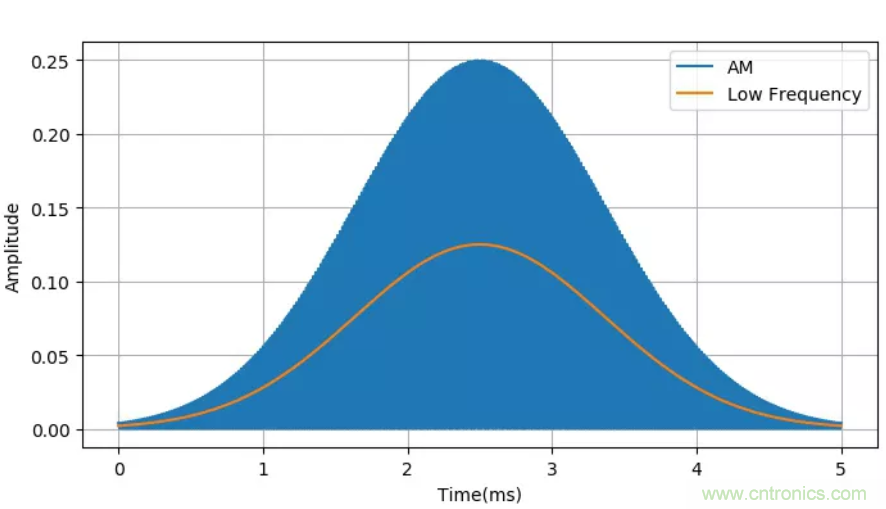
▲ 高斯信號同步解調后的波形
頻率混疊
在前面講述信號的幅度調制與解調過(guò)程中,都是假設信號的頻譜遠遠小于載波的頻率。這樣信號被調制后,它的頻譜搬移到高頻時(shí),左右的頻譜之間沒(méi)有重疊。但是如果調制頻譜低,小于信號中最高頻率,那么調制后的信號頻譜中,左右兩個(gè)搬移后的頻譜之間就會(huì )有混疊。這就為后面進(jìn)行信號恢復埋下了隱患。
下面將前面實(shí)驗中載波的頻率從原來(lái)的30kHz,降低到0.5kHz,給出對應的調制波形。
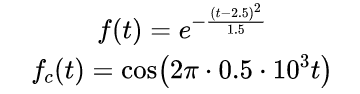
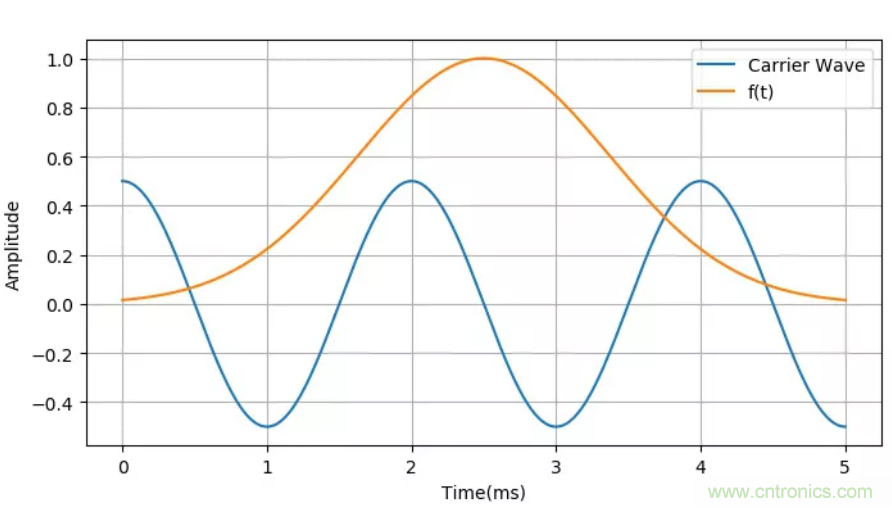
▲ 高斯信號與低頻的載波信號

▲ 高斯信號低頻調幅后的波形
同樣使用同步解調,所得到的信號中,信號本身 與兩倍頻調制的信號
與兩倍頻調制的信號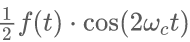 之間頻譜也同樣存在著(zhù)混疊,這樣就會(huì )使得低通濾波器無(wú)法將信號本身恢復出來(lái)了。
之間頻譜也同樣存在著(zhù)混疊,這樣就會(huì )使得低通濾波器無(wú)法將信號本身恢復出來(lái)了。
下圖顯示了上面調幅信號與載波信號相乘之后的結果(藍色的AM曲線(xiàn)),對比原來(lái)的高斯信號(橙色Low Frequency曲線(xiàn)),可以看出使用普通的低通濾波器很難從藍色曲線(xiàn)恢復出橙色曲線(xiàn)了。
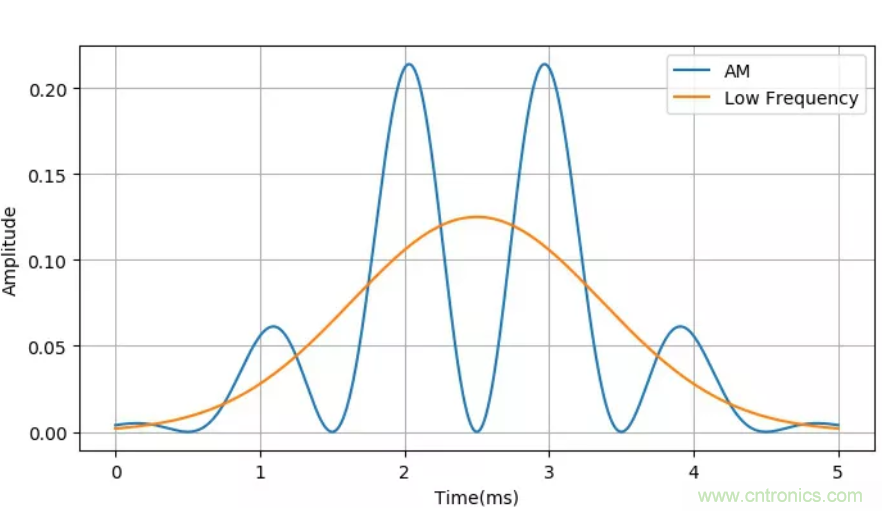
▲ 調幅信號與載波信號乘積之后的信號

▲ 高斯調制信號頻譜混疊示意圖
復震蕩信號調制
為了避免幅度調制后的頻率混疊帶來(lái)信號恢復的困難,在實(shí)踐中,可以采用復震蕩信號調制的方式。也就是將原來(lái)的信號調制在一對相位相差90°(正交)的載波信號上,形成一對正交調制信號。在數學(xué)上,可以將這對信號看成復數的實(shí)部和虛部,所組成的復值信號的頻譜則是原來(lái)信號的頻譜往右平移,自然就沒(méi)有了混疊的問(wèn)題。

▲ 復震蕩信號調制框圖
下面公式表示復指數震蕩信號的調制的過(guò)程:
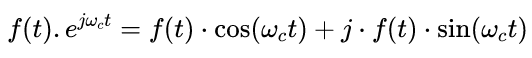
下圖顯示了上面復指數調制后的實(shí)部、虛部?jì)陕沸盘柌ㄐ巍?/div>



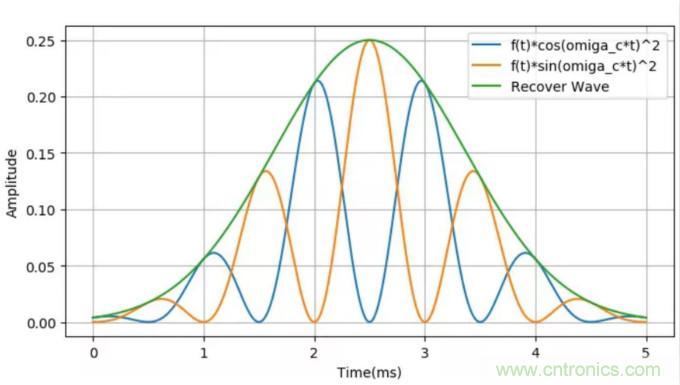
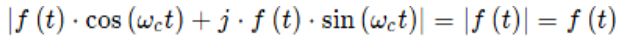

▲ 復指數調制后的兩路波形
如果需要恢復出原來(lái)的信號,則將原來(lái)的信號乘以前面復震蕩信號的共軛信號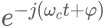 ,所生成信號的實(shí)部就是恢復的原來(lái)信號了。
,所生成信號的實(shí)部就是恢復的原來(lái)信號了。
根據復數的乘法運算,復數乘積的實(shí)部等于原來(lái)兩個(gè)復數的實(shí)部相乘,減去虛部相乘的結果。
因此對應的復指數震蕩信號同步解調過(guò)程就是:

下圖顯示了使用復指數調制后的實(shí)部和虛部分別與 相乘之后的波形(藍色,橙色),他們相加之后的波形(綠色)就是回復后的高斯波形。
相乘之后的波形(藍色,橙色),他們相加之后的波形(綠色)就是回復后的高斯波形。

▲ 進(jìn)行復指數回復后的波形
如果信號f(t) 的幅值始終大于零0,即f(t)≥0,那么從復震蕩調制信號恢復原來(lái)信號還可以簡(jiǎn)單的通過(guò)求復調制信號的幅度來(lái)恢復:
推薦閱讀:




