將有源濾波器視為兩個(gè)級聯(lián)的濾波器是一個(gè)有用的方法。如圖1所示，其中一個(gè)濾波器是理想的濾波器，用于體現傳遞函 數;另一個(gè)是構成濾波器的放大器。在閉環(huán)的負反饋環(huán)路中所采用的放大器可以被視為一個(gè)具有一階響應的、簡(jiǎn)單的低通濾波器。當頻率超過(guò)某一點(diǎn)后，增益將隨著(zhù) 頻率的增長(cháng)而出現滾降現象。此外，如果放大器使用反相放大結構的話(huà)，則所有頻率點(diǎn)上還將出現附加的180°相移。

　　

圖1. 以?xún)蓚€(gè)級聯(lián)的傳遞函數的形式表示的濾波器

　　

濾 波器設計過(guò)程可分為兩步。首先選定濾波器的響應特性，接下來(lái)選出適當的電路結構來(lái)實(shí)現它。濾波器的響應是指衰減曲線(xiàn)的形狀，這常?？梢詺w為經(jīng)典的響應特性 中的一種，如Butterworth、Bessel或者某種Chebyshev型。雖然這些響應特性的選擇往往會(huì )影響幅值響應特性，但它們也會(huì )影響相位響 應特性的形狀。在本文中，為了進(jìn)行比較，忽略幅值響應，認為其幾乎不變。

　　

濾波器的復雜性往往通過(guò)濾波器的“階數”來(lái)定義，該參數與儲能元 件(電感和電容)的數量有關(guān)。濾波器傳遞函數分母的階數定義了隨著(zhù)頻率的上升而呈現的衰減速率。漸近線(xiàn)型的濾波器滾降速率為-6ndB/倍頻程，或者 -20ndB/十倍頻程，其中n是極點(diǎn)的數量。倍頻程是指頻率的二倍或者一半，十倍頻程是頻率的十倍增長(cháng)或者縮減。因此，一個(gè)一階(或者單極點(diǎn))濾波器的 滾降速率為-6dB/倍頻程或者-20dB/十倍頻程。類(lèi)似的，一個(gè)二階(或者2極點(diǎn))濾波器的滾降速率為-12dB/倍頻程或者-40dB/十倍頻程。 更高階次的濾波器往往是由級聯(lián)的一階和二階基本單元所構成的。自然，我們可以利用單個(gè)有源放大電路級來(lái)構建三階、甚至四階濾波器，但是對于元件值的敏感， 以及元件之間的相互作用對頻率響應所造成影響的大幅度上升，會(huì )使這些選擇不那么具有吸引力。

　　

傳遞函數

　　

首先，我們考察一下傳遞函數的相位響應。對于同樣階數的濾波器選項來(lái)說(shuō)，它們的傳遞函數的相移特性都相同。

　　

對于單極點(diǎn)、低通的情形，傳遞函數的相移為φ，由下式給出。

　　

　　

式中：ω = 頻率(弧度/秒)

　　

ω0 = 中心頻率(弧度/秒)

　　

以弧度/秒為單位的頻率等于2π乘以以Hz為單位的頻率，這是因為每個(gè)360°周期對應著(zhù)2π弧度。由于上面的表達式是一個(gè)無(wú)量綱的比值，故f和ω都可以采用。

　　

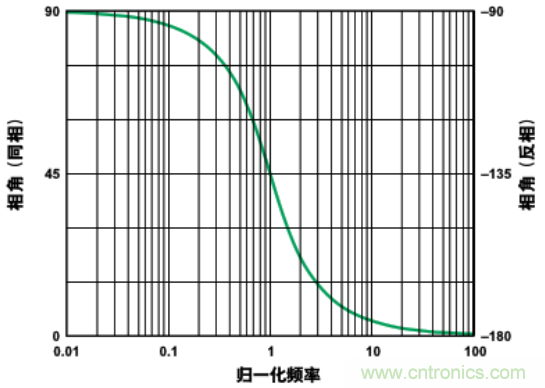
中心頻率還可以被稱(chēng)為截止頻率(即該單極點(diǎn)、低通濾波器的幅值響應特性下降3dB——約30%——的頻率點(diǎn))。在相位關(guān)系方面，中心頻率是相移量達到其最終 值-–90°(在這個(gè)例子中)的50%時(shí)的頻率點(diǎn)。圖2是一幅半對數圖，描述了公式1所表述的相位響應關(guān)系，其頻率范圍是中心頻率以下的兩個(gè)十倍頻程至中心頻率以上的兩個(gè)十倍頻程。中心頻率(=1)處的相位移動(dòng)為–45°。

　　

圖2. 一個(gè)單極點(diǎn)、低通濾波器在中心頻率附近的相位響應(同相，左軸;反相響應，右軸) 

 

類(lèi)似的，一個(gè)單極點(diǎn)的高通濾波器可以由下式給出：

　　

 

圖3描繪了公式2所表示的、在中心頻率以下兩個(gè)十倍頻程至中心頻率以上兩個(gè)十倍頻程這一范圍內的響應特性。其歸一化的中心頻率(=1)處的相移為+45°。

　　

顯然，高通和低通特性類(lèi)似，只是相互間存在90°的相位差(π/2 radians)

　　

圖3. 一個(gè)單極點(diǎn)、低通濾波器在中心頻率 1 附近的相位響應(同相，左軸;反相響應，右軸)

　　

對于二階、低通的情形，傳遞函數的相移可以由下式近似表示為

　　

 

式中α是濾波器的阻尼比。它將決定幅值響應曲線(xiàn)上的峰值以及相位曲線(xiàn)過(guò)渡段的陡峭程度。它是電路的Q值的倒數，這也決定了幅值滾降或相位偏移的陡峭程度。 Butterworth響應的α為1.414(Q=0.707)，可以產(chǎn)生最大平坦度響應特性。更低的α會(huì )使幅值響應特性曲線(xiàn)上出現尖峰。

　　

圖4. 一個(gè)雙極點(diǎn)、低通濾波器的中心頻率 1 附近的相位響應(同相，左軸;反相響應，右軸)

　　

圖4描繪了該式所表示的(α=1.414)、在中心頻率以下兩個(gè)十倍頻程至中心頻率以上兩個(gè)十倍頻程這一范圍內的響應特性。這里，中心頻率(=1)處出現的相位偏移為–90°。

 

一個(gè)2極點(diǎn)、高通濾波器的相位特性響應可以由下式近似表示

　　

 

圖5描繪了該式所表示的響應特性(同樣有α=1.414)，其范圍是中心頻率(=1)以下兩個(gè)十倍頻程至中心頻率以上兩個(gè)十倍頻程，相應的相移為

　　

圖5. 一個(gè)雙極點(diǎn)、高通濾波器的中心頻率1附近的相位響應(同相，左軸;反相響應，右軸)

 

同樣的，顯然高通和低通相位響應是類(lèi)似的，僅僅存在180°的相位偏移(π弧度)。

 

在更高階數的濾波器中，每個(gè)附加段的相位響應都累加到總的相移量之上。這一特性將在下面進(jìn)一步予以討論。為了與通常的實(shí)踐保持一致，所示出的相移被限制為±180°的范圍之內。例如，–181°事實(shí)上等價(jià)于 +179°，360°等價(jià)于0°，依此類(lèi)推。

　　

一階濾波器段

　　

一階濾波器段可以以多種方式來(lái)構建。 圖6示出最簡(jiǎn)單的一種結構，即使用無(wú)源的R-C架構。該濾波器的中心頻率為1/(2πRC)。它之后往往接一個(gè)同相的緩沖放大器，以防止濾波器之后的電路 對其產(chǎn)生負載效應，負載會(huì )改變?yōu)V波器的響應特性。此外，緩沖器還可以提供一定的驅動(dòng)能力。相位響應如圖2所示，即在中心頻率點(diǎn)處產(chǎn)生45°的相移，正如傳 遞函數所預測的那樣，這是因為沒(méi)有另外的元件改變相移特性。這種響應特性將被稱(chēng)為同相、一階、低通響應特性。只要緩沖器的帶寬顯著(zhù)高于濾波器，那么緩沖器 就不會(huì )帶來(lái)相移。

　　

圖6. 無(wú)源低通濾波器

　　

請記住，這些圖中的頻率值是歸一化的，即相對于中心頻率的比值。例如，若中心頻率是5kHz，則這些圖將展示50Hz到500kHz范圍內的相位響應特性。

　　

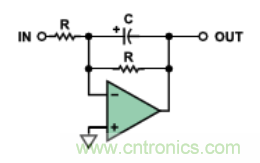
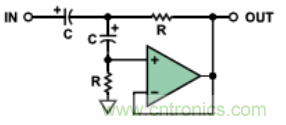
圖 7示出另外一種結構。該電路增加了一個(gè)并聯(lián)電阻，對積分電容進(jìn)行連續放電，從根本上來(lái)說(shuō)它是一個(gè)有損耗的積分器。其中心頻率同樣是1/(2πRC)。因為 該放大器是以反相模式工作的，故反相模式將在相移特性上引入附加的180°相位。圖2示出了輸入-輸出的相位差隨頻率的變化，其中包括了放大器引入的反相 (右軸)。該響應特性將被稱(chēng)為反相的、一階、低通響應。

　　

圖7. 利用工作在反相模式的運放搭建的有源、單極點(diǎn)、低通濾波器

　　

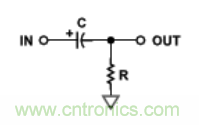
上面所示的電路可以衰減高頻分量而通過(guò)低頻分量，均屬于低通濾波器?？梢酝ㄟ^(guò)高頻分量的電路則與之類(lèi)似。圖8示出一個(gè)無(wú)源的一階、高通濾波器電路結構，其相位隨著(zhù)歸一化頻率的變化特性則示于圖3中(同相響應)。

　

　

圖8. 無(wú)源高通濾波器

　　

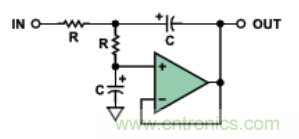
圖3(左軸)的曲線(xiàn)被稱(chēng)為同相、一階、高通響應特性。該高通濾波器的有源電路示于圖9中。其相位隨頻率的變化示于圖3中(右軸)。這將被稱(chēng)為反相、一階、高通響應。

　　

圖9. 有源、單極點(diǎn)、高通濾波器

 

二階濾波器段

　　

二階濾波器有各式各樣的電路結構。這里要討論的是Sallen-Key、多路反饋、狀態(tài)變量結構，及其類(lèi)似的雙二階濾波結構。它們是最常見(jiàn)的結構，而且與本文的內容相關(guān)。關(guān)于各種不同結構的更為完整的信息可參見(jiàn)文后的參考文獻。

　　

Sallen-Key低通濾波器

　　

廣 泛使用的Sallen-Key結構也被稱(chēng)為電壓控制電壓源(VCVS)型，是MIT的林肯實(shí)驗室(參見(jiàn)文獻3)的R.P. Sallen和 E.L. Key于1955年提出的結構。圖10示出了一個(gè)Sallen-Key二階低通濾波器的電路原理圖。這一結構受到廣泛歡迎的一個(gè)原因是它的性能基本與運放 的性能無(wú)關(guān)，因為放大器主要作為一個(gè)緩沖器來(lái)使用。由于在基本的Sallen-Key電路中，連接成跟隨器的運放并不用于產(chǎn)生電壓增益，故對它的增益-帶 寬要求并不重要。這意味著(zhù)，對于給定的運放帶寬而言，與運放的動(dòng)態(tài)特性受到可變反饋環(huán)路特性影響的那些電路結構相比，利用這一固定的(單位)增益可以設計 出頻率更高的濾波器。通過(guò)濾波器后，信號的相位保持不變(同相結構)。圖4示出一個(gè)Q=0.707(或者，阻尼比α=1/Q=1.414—— Butterworth響應特性)的Sallen-Key低通濾波器的相移-頻率關(guān)系圖。為了簡(jiǎn)化比較，這將作為下面所考慮的二階濾波器段的性能標準。

　　

圖10. 2極點(diǎn)、Sallen-Key低通濾波器

　　

Sallen-Key高通濾波器

　　

通過(guò)互換決定頻率網(wǎng)絡(luò )上的電容和電阻的位置，可將Sallan-Key低通電路變換為高通結構，正如圖11所示的那樣，而且同樣采用單位增益的緩沖器。其相移-頻率關(guān)系示于圖5中(左軸)。這是同相、二階、高通響應。

　　

圖11. 2極點(diǎn)、Sallen-Key高通濾波器

　　

Sallen-Key濾波器的放大器增益可以通過(guò)在運放反相輸入上連接一個(gè)電阻衰減器組成的反饋網(wǎng)絡(luò )來(lái)提高。不過(guò)，改變增益將影響到?jīng)Q定頻率網(wǎng)絡(luò )的表達式，而且需要重新計算元件的值。該放大器的動(dòng)態(tài)特性也需要更嚴格的考察，因為它們在環(huán)路中引入了增益。

　　

多路反饋(Multiple-Feedback，MFB)低通濾波器

　　

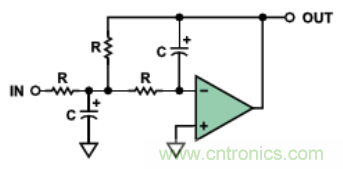
多路反饋濾波器是一種單放大器電路結構，反饋環(huán)路是基于運放的積分器(反相配置)，如圖12所示。因此，運放參數對傳遞函數之間的影響要大于 Sallen-Key的實(shí)現方案。要產(chǎn)生一個(gè)高Q、高頻電路是很困難的，因為運放在高頻段的開(kāi)環(huán)增益有限。一條指導方針是，運放的開(kāi)環(huán)增益應該至少比諧振 (或者截止)頻率處的幅值響應高出20dB(即10倍于之)，包括濾波器的Q值造成的峰值。由于Q值而造成的尖峰將具有如下的幅值

　　

 

式中：H是電路的增益。

　　

 

圖12. 2極點(diǎn)、多路反饋(MFB)、低通濾波器

　　

該多路反饋濾波器會(huì )使信號反相。這等價(jià)于讓濾波器自身的相移增加了180°。圖4示出了相位-頻率變化關(guān)系(右軸)。這將被稱(chēng)為反相、二階、低通響應。值得 注意的是，在得到給定響應特性的條件下，多路反饋結構中的最大和最小元件值之間的差異要大于Sallen-Key實(shí)現方案中的。

　　

多路反饋(MFB)、高通濾波器

　　

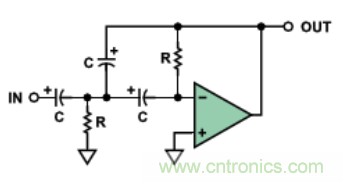
上面關(guān)于多路反饋、低通濾波器的評述也適用于高通的情形。圖13示出一個(gè)多路反饋、高通濾波器的原理圖，其理想的相移-濾波特性則示于圖5中(右軸)。這被稱(chēng)為反相、二階、高通響應特性。

　　

圖13. 2極點(diǎn)、多路反饋(MFB)高通濾波器

　　

要保證這種濾波器的具體電路實(shí)現在高頻情況下的穩定性是十分困難的，因為它是在一個(gè)微分器的基礎上構建的，與所有的微分器電路所類(lèi)似的是，它在更高的頻率上閉環(huán)增益更大，因此會(huì )對噪聲產(chǎn)生放大作用。

　　

狀態(tài)變量型濾波器

　　

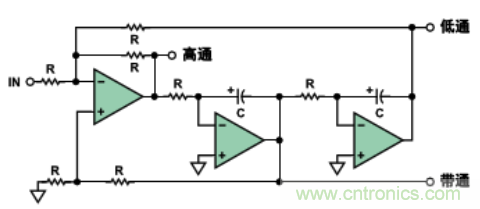
圖14示出了一種狀態(tài)變量實(shí)現方案。該結構是最靈活和最精確的實(shí)現方案，付出的代價(jià)是電路元件的數量大大增加，其中包括了3個(gè)運放。所有3個(gè)主要的參數(增益、Q和ω0)都可以獨立調節，而且可以同時(shí)提供低通、高通和帶通輸出。該濾波器的增益也是獨立的變量。

　　

由于狀態(tài)變量濾波器的所有參數都可以獨立調節，故其元件值的散布變得很小。而且由于溫度和元件公差所帶來(lái)的失配也可以最小化。與上面的多路反饋電路類(lèi)似的是，積分器部分所使用的運放的增益帶寬積也成為電路的限制條件。

　　

圖14. 2極點(diǎn)、狀態(tài)變量濾波器

　　

其中低通濾波段的相移-頻率特性屬于一個(gè)反相的二階型響應(參見(jiàn)圖4，右軸)，高通段電路將具有反相高通響應(參見(jiàn)圖5，右軸)。

　　

雙二階(biquad)

　　

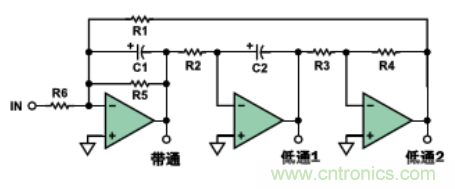
狀 態(tài)變量濾波器的一個(gè)近親是雙二階型(參見(jiàn)圖15)。該電路的名稱(chēng)最早是由J. Tow于1968年使用的(見(jiàn)參考文獻6)，后來(lái)由L.C. Thomas 于1971年使用(見(jiàn)文獻5)，其工作是基于如下的事實(shí)：傳遞函數是兩個(gè)二階項之比。該電路與狀態(tài)變量電路之間存在輕微的區別。在這一結構中，不能提供單 獨的高通輸出。不過(guò)它具有兩路低通輸出，其中一路是同相的(LOWPASS1)，另一路是反相的(LOWPASS2)。

　　

圖15. 標準的雙二階2極點(diǎn)電路

　　

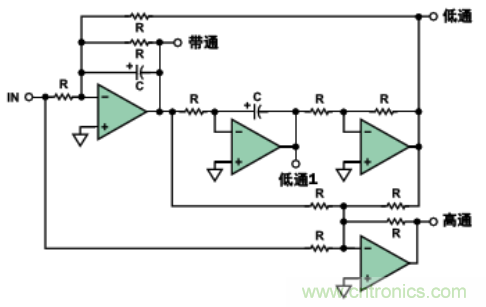
由于添加了第四個(gè)放大器電路，故可以實(shí)現高通、陷波(低通、標準和高通)以及全通型濾波器。圖16示出一個(gè)帶有高通電路的雙二階電路的原理圖。

　　

圖16. 2極點(diǎn)雙二階濾波器(帶有高通段)

　　

其中LOWPASS1段的相移-頻率特性屬于同相、二階、低通型響應(參見(jiàn)圖4的左軸)。LOWPASS2段將具有反相的二階型響應(參見(jiàn)圖4，右軸)。HIGHPASS段的相移特性屬于反相特性(參見(jiàn)圖5，右軸)。

 

結論

　　

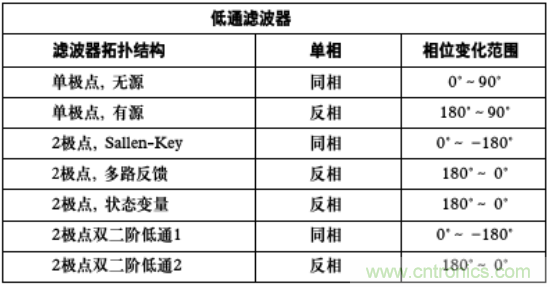
我們已經(jīng)看到用于構建一個(gè)濾波器的拓撲將影響其實(shí)際的相位響應。這會(huì )是確定所用的拓撲時(shí)需要考慮的一個(gè)因素。表1對本文中討論的各種低通濾波器結構的相移范圍進(jìn)行了比較。

　　

表1 低通濾波器架構的相移范圍

 

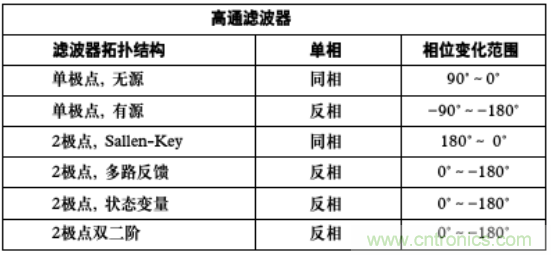
類(lèi)似的，表2對各種高通濾波器結構進(jìn)行了比較。 

　　

表2 高通濾波器拓撲相移范圍

 

相移特性隨Q的變化特性

　　

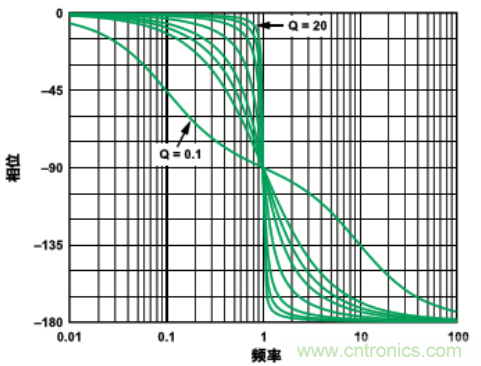
上述的2階響應的Q值都是0.707。圖17示出了Q的變化對低通濾波器的相位響應的影響(對高通濾波器的影響也 類(lèi)似)。圖中繪出了Q = 0.1，0.5，0.707，1，2，5，10和20時(shí)的相位響應曲線(xiàn)。值得注意的是，Q值較低的情況下，在遠低于截止頻率的頻率上相位就開(kāi)始發(fā)生變化。

　　

圖17. 相移隨Q值的變化特性

　　

雖然幅值響應隨Q值的變化并非本文的主題，但也是一個(gè)令人感興趣的問(wèn)題。圖18示出了Q值在上述范圍內變化時(shí)一個(gè)2階濾波器的幅值響應特性。

　　

當高Q電路應用于多級濾波器時(shí)，高Q電路的響應特性的尖峰現象也是令人感興趣的問(wèn)題。雖然在理論上這些電路段以何種順序來(lái)級聯(lián)并無(wú)差異，而在實(shí)踐中，把Q值 較低的電路段置于高Q電路段之前將更為有利，這是為了讓尖峰現象不致于超出濾波器的動(dòng)態(tài)范圍。雖然該圖是針對低通段的，但高通響應也存在類(lèi)似的尖峰。

　　

圖18. 隨著(zhù)Q值的變化，2極點(diǎn)濾波器的幅值尖峰特性的變化

 

高階次濾波器

　　

傳遞函數可以級聯(lián)起來(lái)，構成更高階次的響應特性。當濾波器響應串連起來(lái)后，其在任意頻率上的dB增益(以及衰減)和相角都相加起來(lái)。正如我們在前面指出的那 樣，多極點(diǎn)濾波器一般是利用級聯(lián)的二階電路段搭建的，對于奇次階濾波器，可以另外添加一段一階電路。兩個(gè)級聯(lián)的一階電路段并不能像單個(gè)二階濾波段那樣提供 很寬的Q值變化范圍。

　　

圖19示出一個(gè)通過(guò)傳遞函數級聯(lián)所構成的4階濾波器。這里，我們可以看到，濾波器是由兩個(gè)二階段所構成的。

　　

圖19. 傳遞函數的級聯(lián)所構成的4極點(diǎn)濾波器

　　

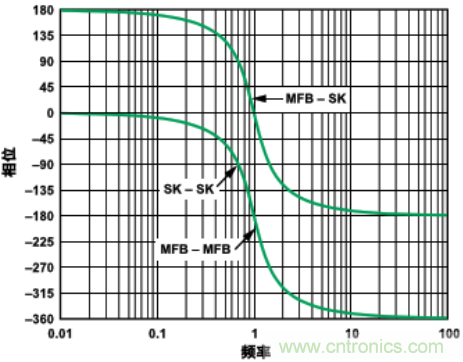
圖 20示出了構建一個(gè)4階濾波器的3種方式對相位響應的影響。第一種結構是利用兩個(gè)Sallen-Key(SK)Butterworth段搭建的。第二種是 利用兩個(gè)多路反饋(MFB) Butterworth段搭建的。第三種是利用一個(gè)SK段和一個(gè)MFB段搭建的。但是，正如兩個(gè)級聯(lián)的一階電路段并不能構成一個(gè)二階電路段一樣，2個(gè)級聯(lián) 的2階Butterworth段并不能等效于一個(gè)4階Butterworth段。第一段Butterworth濾波器的f0為1，Q值為0.5412(α=1.8477)。第二段的f0為1，Q值為1.3065(α=0.7654)。

　　

正如前面所提到過(guò)的那樣，SK段是同相型的，而MFB是反相型的。圖20對這3種4階電路的相移特性進(jìn)行了比較。其中SK和MFB濾波器具有相同的相位響應 特性，因為兩個(gè)反相段產(chǎn)生了同相響應(-1×-1=+1)。利用混合拓撲結構(SK和MFB)構建的濾波器的響應特性將偏移180° (+1 ×–1 = –1)。

　　

圖20. 不同結構的4階電路的相位響應

　　

請注意，正如可以預料到的那樣，總的相移特性是一個(gè)2階電路段的兩倍360° vs. 180°。高通濾波器將擁有類(lèi)似的相位響應，但偏移相差180°。

　　

該級聯(lián)的思想可以用來(lái)搭建更高階次的濾波器，但是，在實(shí)踐中，超過(guò)8階的濾波器很難實(shí)現。將來(lái)的文章將對帶通、陷波(帶阻)和全通濾波器的相位關(guān)系進(jìn)行考察。

 

 

推薦閱讀：